【题目】阳光小区附近有一块长100m,宽80m的长方形空地,在空地上有两条相同宽度的步道(一纵一横)和一个边长为步道宽度7倍的正方形休闲广场,两条步道的总面积与正方形休闲广场的面积相等,如图1所示.设步道的宽为a(m).

(1)求步道的宽.
(2)为了方便市民进行跑步健身,现按如图2所示方案增建塑胶跑道.己知塑胶跑道的宽为1m,长方形区域甲的面积比长方形区域乙大441m2, 且区域丙为正方形,求塑胶跑道的总面积.
参考答案:
【答案】(1)3.6m (2)199m2
【解析】
(1)步道宽度为a, 则正方形休闲广场的边长为7a, 根据两条步道总面积等于休闲广场面积列方程求解即可.其中注意两条步道总面积要减去重叠部分的小正方形面积.
(2)根据空地的长度和宽度,道路和塑胶的宽度以及丙的边长,计算出甲、乙区域长之差,因两区域的宽度相等,根据面积之差等于长度之差乘以宽度,求得宽度,即正方形丙的边长,塑胶跑道的总面积等于总长度乘以塑胶宽度,总长度等于空地长宽之和加丙的一边长,再减去有两次重复相加的塑胶宽度.
(1)解:由题意,得100a+80a-a2=(7a)2 ,
化简,得a2=3.6a,
∵a>0,
∴a=3.6.
答:步道的宽为3.6 m.
(2)解:如图,
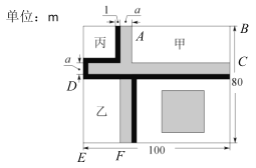
由题意,得AB-DE=100-80+1=21(m),
∴BC=EF=![]() =21(m).
=21(m).
∴塑胶跑道的总面积为1×(100+80+21-2)=199(m2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知平面内有A、B、C、D四点,请按下列要求作图.

(1)作射线AC,线段DC;
(2)作∠BAD的补角,并标上字母;
(3)用量角器量出∠BAC的度数,并求出它的余角的度数(精确到度);
(4)在图中求作一点P,使P点到A、B、C、D四点的距离和最短.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,线段AB=CD,AB与CD相交于点O,且∠AOC=60°,CE是由AB平移所得,AC与BD不平行,则AC+BD与AB的大小关系是:AC+BD_____AB.(填“>”“<”或“=”)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°.

(1)请你数一数,图中有______个小于平角的角;
(2)求出∠BOD的度数;
(3)请通过计算说明OE是否平分∠BOC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C在线段AB上,过点C作CD⊥AB,点E,F分别是AD,CD的中点,连结EF并延长EF至点G,使得FG=CB,连结CE,GB,过点B作BH∥CE交线段EG于点H.
(1)求证:四边形FCBG是矩形.
(2)己知AB=10,
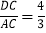 .
. ①当四边形ECBH是菱形时,求EG的长.
②连结CH,DH,记△DEH的面积为S1, △CBH的面积为S2.若EG=2FH,求S1+S2的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某物流公司现有114吨货物,计划同时租出A,B两种型号的车,王经理发现一个运货货单上的一个信息是:
A型车(满载)
B型车(满载)
运货总量
3辆
2辆
38吨
1辆
3辆
36吨
根据以上信息,解析下列问题:
(1)1辆A型车和1辆B型车都装满货物一次可分别运货多少吨?
(2)若物流公司打算一次运完,且恰好每辆车都装满货物,请你帮该物流公司设计租车方案。
-
科目: 来源: 题型:
查看答案和解析>>【题目】周末,小李从家里出发骑车到少年宫学习绘画,学完后立即回家,他离家的距离y(km)与时间x(h)之间的函数关系如图所示,有下列结论:①他家离少年宫30km;②他在少年宫一共停留了3h;③他返回家时,离家的距离y(km)与时间x(h)之间的函数表达式是y=-20x+110;④当他离家的距离y=10时,时间x=
 .其中正确的是________(填序号).
.其中正确的是________(填序号).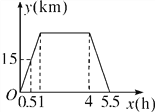
相关试题

