【题目】如图,点C在线段AB上,过点C作CD⊥AB,点E,F分别是AD,CD的中点,连结EF并延长EF至点G,使得FG=CB,连结CE,GB,过点B作BH∥CE交线段EG于点H.
(1)求证:四边形FCBG是矩形.
(2)己知AB=10,![]() .
.
①当四边形ECBH是菱形时,求EG的长.
②连结CH,DH,记△DEH的面积为S1, △CBH的面积为S2.若EG=2FH,求S1+S2的值.

参考答案:
【答案】(1)证明见解析 (2)①![]() ②16或
②16或![]()
【解析】
(1)由EF是中位线,得EF平行AB,即FG平行CB,已知FG=CB,由一组对边平行且相等得四边形FCBG是平行四边形,又因为CD垂直AB,则四边形FCBG是矩形.
(2)①因为EF平行AC,根据平行列比例式,设EF为3x, 由中位线性质,直角三角形的中线的性质,四边形ECBH是菱形等条件,通过线段的长度转化,最终把AC和BC用含x的关系式表示,由AB=8,列方程,求出x, 把EG也用含x的代数式表示,代入x值,即可求出EG的长.
②由EF是△ACD的中位线,得DF=CF,根据同底等高三角形面积相等,得△DEH和△CEH的面积相等,因为四边形CEHB是平行四边形,所以△CEH的面积和△BCH的面积相等,得到关系式:S1+S2=2S2,由EF+FH=FH+HG,得EF=HG,结合已知EG=2FH,得FH=2FG,设EF等于a, 把有关线段用含a的代数式表示,分两种情况,即点H在FG上和点H在EF上,根据AB=10列关系式,求出a的值,再把S2用含a的代数式表示,代入a值即可.
(1)∵EF即是△ADC的中位线,
∴EF∥AC,即FG∥CB.
∵FG=CB,
∴四边形FCBG是平行四边形.
∵CD⊥AB,即∠FCB=90°,
∴四边形FCBG是矩形.
(2)解:①∵EF是△ADC的中位线,
∴EF=![]() AC,DF=
AC,DF=![]() CD,
CD,
∴ ![]()
∴可设EF=3x,则DF=CF=4x,AC=6x.
∵∠EFC=90°,
∴CE=5x.
∵四边形ECBH是菱形,
∴BC=EC=5x,
∴AB=AC+CB=6x+5x=10,
∴x=![]()
∴EG=EF+FG=EF+BC=3x+5x=8x=![]() ;
;
②∵EH∥BC,BH∥CE,
∴四边形ECBH是平行四边形,
∴EH=BC,
又∵DF=CF,
∴S△DEH=S△CEH ,
∵四边形ECBH是平行四边形,
∴S△CEH=S△BCH
∴S1+S2=2S2 .
∵EH=BC=FG,
∴EF=HG.
当点H在线段FG上时,如图,
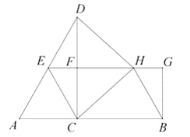
设EF=HG=a,∵EG=2FH,
∴EG=2FH=4a,AC=2EF=2a,
∴BC=FG=3a.
∴AB=AC+C=2a+3a=10,
∴a=2.
∵FC=![]() AC=
AC=![]() a,
a,
∴S1+S2=2S2=2×![]() ×3a×
×3a×![]() a=4a2=16.
a=4a2=16.
当点H在线段EF上时,如图.
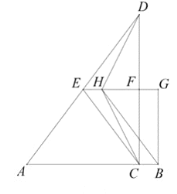
设EH=FG=a,则HF=2a.
同理可得AC=6a,BC=a,FC=4a,
∴AB=6a+a=10,
∴a= ![]()
∴S1+S2=2S2=2×![]() ×a×4a=4a2=
×a×4a=4a2= ![]() .
.
综上所述,S1+S2的值是16或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,线段AB=CD,AB与CD相交于点O,且∠AOC=60°,CE是由AB平移所得,AC与BD不平行,则AC+BD与AB的大小关系是:AC+BD_____AB.(填“>”“<”或“=”)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°.

(1)请你数一数,图中有______个小于平角的角;
(2)求出∠BOD的度数;
(3)请通过计算说明OE是否平分∠BOC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阳光小区附近有一块长100m,宽80m的长方形空地,在空地上有两条相同宽度的步道(一纵一横)和一个边长为步道宽度7倍的正方形休闲广场,两条步道的总面积与正方形休闲广场的面积相等,如图1所示.设步道的宽为a(m).

(1)求步道的宽.
(2)为了方便市民进行跑步健身,现按如图2所示方案增建塑胶跑道.己知塑胶跑道的宽为1m,长方形区域甲的面积比长方形区域乙大441m2, 且区域丙为正方形,求塑胶跑道的总面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某物流公司现有114吨货物,计划同时租出A,B两种型号的车,王经理发现一个运货货单上的一个信息是:
A型车(满载)
B型车(满载)
运货总量
3辆
2辆
38吨
1辆
3辆
36吨
根据以上信息,解析下列问题:
(1)1辆A型车和1辆B型车都装满货物一次可分别运货多少吨?
(2)若物流公司打算一次运完,且恰好每辆车都装满货物,请你帮该物流公司设计租车方案。
-
科目: 来源: 题型:
查看答案和解析>>【题目】周末,小李从家里出发骑车到少年宫学习绘画,学完后立即回家,他离家的距离y(km)与时间x(h)之间的函数关系如图所示,有下列结论:①他家离少年宫30km;②他在少年宫一共停留了3h;③他返回家时,离家的距离y(km)与时间x(h)之间的函数表达式是y=-20x+110;④当他离家的距离y=10时,时间x=
 .其中正确的是________(填序号).
.其中正确的是________(填序号).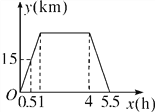
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠ABC=∠ADC=90°,BD平分∠ABC,∠DCB=60°,AB+BC=8,则AC的长是_____.

相关试题

