搜索
【题目】如图，在以O为原点的直角坐标系中，矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上，反比例函数y= 
（x＞0）与AB相交于点D，与BC相交于点E，若BD=3AD，且△ODE的面积是9，则k=（ ）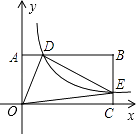
A.
B.
C.
D.12
参考答案：
【答案】C
【解析】解：∵四边形OCBA是矩形，
∴AB=OC，OA=BC，
设B点的坐标为（a，b），
∵BD=3AD，
∴D（ 
，b），
∵点D，E在反比例函数的图象上，
∴ 
=k，∴E（a， 
），
∵S△ODE=S矩形OCBA﹣S△AOD﹣S△OCE﹣S△BDE=ab﹣ 
﹣ ﹣ 
（b﹣ ）=9，
∴k= 
，
所以答案是：C．
【考点精析】解答此题的关键在于理解反比例函数的性质的相关知识，掌握性质:当k＞0时双曲线的两支分别位于第一、第三象限，在每个象限内y值随x值的增大而减小； 当k＜0时双曲线的两支分别位于第二、第四象限，在每个象限内y值随x值的增大而增大，以及对三角形的面积的理解，了解三角形的面积=1/2×底×高．
-
科目： 来源： 题型：
查看答案和解析>>【题目】【发现证明】如图1，点E，F分别在正方形ABCD的边BC，CD上，∠EAF=45°，试判断BE，EF，FD之间的数量关系．
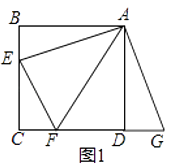
小聪把△ABE绕点A逆时针旋转90°至△ADG，通过证明△AEF≌△AGF；从而发现并证明了EF=BE+FD．
（1）【类比引申】如图2，点E、F分别在正方形ABCD的边CB、CD的延长线上，∠EAF=45°，连接EF，请根据小聪的发现给你的启示写出EF、BE、DF之间的数量关系，并证明；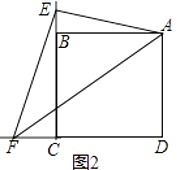
（2）【联想拓展】如图3，如图，∠BAC=90°，AB=AC，点E、F在边BC上，且∠EAF=45°，若BE=3，EF=5，求CF的长．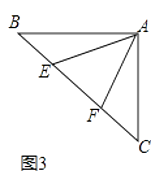
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知一次函数 y=kx+b 的图象经过点（-1，-5），且与正比例函数
于点（2，a），求:（1）a 的值；
（2）k，b 的值；
（3）这两个函数图象与 x 轴所围成的三角形的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某同学在用描点法画二次函数y=
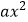+bx+c的图象时，列出了下面的表格：x
…
﹣2
﹣1
0
1
2
…
y
…
﹣11
﹣2
1
﹣2
﹣5
…
由于粗心，他算错了其中一个y值，则这个错误的数值是（ ）.
A．﹣11 B．﹣2 C．1 D．﹣5 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知AC⊥BC，BD⊥AD，AC 与BD 交于O，AC=BD．
求证：（1）BC=AD；
（2）△OAB是等腰三角形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】老师所留的作业中有这样一个分式的计算题：
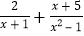，甲、乙两位同学完成的过程分别如下：
老师发现这两位同学的解答都有错误．
(1)甲同学的解答从第 步开始出现错误，错误的原因是 ；
乙同学的解答从第 步开始出现错误，错误的原因是 ；
(2)请重新写出完成此题的正确解答过程．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，直线y=kx+b经过点A（﹣30，0）和点B（0，15），直线y=x+5与直线y=kx+b相交于点P，与y轴交于点C．
（1）求直线y=kx+b的解析式．
（2）求△PBC的面积．
相关试题
