Question

【题目】如图,△ABC中,AB=BC=AC=12cm,现有两点M、N分别从点A. 点B同时出发,沿三角形的边运动，已知点M的速度为1cm/s，点N的速度为2cm/s.当点N第一次到达B点时，M、N同时停止运动.

(1)点M、N运动_________秒后，△AMN是等边三角形?

(2)点M、N在BC边上运动时，运动_______秒后得到以MN为底边的等腰三角形△AMN?

(3)M、N同时运动几秒后，△AMN是直角三角形？请说明理由.

Answer 1

【答案】（1）4；（2）16；（3）M、N同时运动3，，15，18秒后，△AMN是直角三角形，理由见解析.

【解析】

（1）根据题意设点M、N运动t秒后，可得到等边三角形△AMN，然后表示出AM，AN的长，由于∠A等于60°，所以只要AM=AN三角形ANM就是等边三角形；

（2）由△AMN是等腰三角形，可证出△ACM≌△ABN，可得CM=BN，设出运动时间，表示出CM，NB，NM的长，列出方程，可解出未知数的值；

（3）分点N在AB，AC，BC上运动的三种情况，再分别就∠AMN=90°和∠ANM=90°列方程求解可得．

解：（1）设点M、N运动t秒后，可得到等边三角形△AMN，如图1，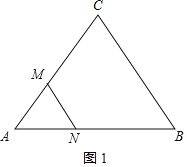

AM=t，AN=12-2t，
∵AB=BC=AC，
∴△ACB是等边三角形，

∴∠A=60°，

当AM=AN时，△AMN是等边三角形
∴t=12-2t，
解得t=4，
∴点M、N运动4秒后，△AMN是等边三角形；

（2）设当点M、N在BC边上运动时，运动t秒后得到以MN为底边的等腰三角形△AMN，
由题意知12秒时M、N两点重合，恰好在C处，
如图2，假设△AMN是等腰三角形，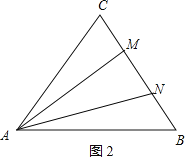

∴AM=AN，
∴∠AMN=∠ANM，
∴∠AMC=∠ANB，
∵AB=BC=AC，
∴△ACB是等边三角形，
∴∠C=∠B，
在△ACM和△ABN中，
∵∠AMC =∠ANB，∠C=∠B，AC=AB
∴△ACM≌△ABN（AAS），
∴CM=BN，
∴t-12=36-2t，
解得t=16，符合题意．
所以点M、N在BC边上运动时，运动16秒后能得到以MN为底的等腰三角形；

（3）①当点N在AB上运动时，如图3，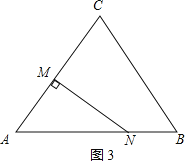

若∠AMN=90°，∵BN=2t，AM=t，
∴AN=12-2t，
∵∠A=60°，
∴2AM=AN，即2t=12-2t，
解得t=3；
如图4，若∠ANM=90°，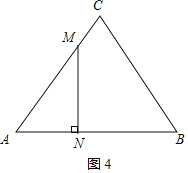

由2AN=AM得2（12-2t）=t，
解得t=；
②当点N在AC上运动时，点M也在AC上，此时A，M，N不能构成三角形；

③当点N在BC上运动时，如图5，

当点N位于BC中点处时，由△ABC时等边三角形知AN⊥BC，即△AMN是直角三角形，
则2t-24=6，
解得t=15；
如图6，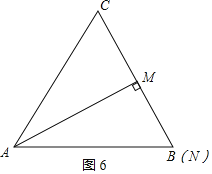

当点M位于BC中点处时，由△ABC时等边三角形知AM⊥BC，即△AMN是直角三角形，
则t-12=6

解得t=18；
综上， M、N同时运动3，，15，18秒后，△AMN是直角三角形；
故答案为：3，，15，18．