【题目】顺次连接平面上A、B、C、D四点得到一个四边形,从①AB∥CD,②BC=AD,③∠A=∠C,④∠B=∠D四个条件中任取其中两个,不能得出“四边形ABCD是平行四边形”这一结论的是( )
A. ①②B. ①③C. ①④D. ③④
参考答案:
【答案】A
【解析】
根据平行四边形的判定定理可得出答案.
解;当①AB∥CD,③∠A=∠C时,四边形ABCD为平行四边形;
当①AB∥CD,④∠B=∠D时,四边形ABCD为平行四边形;
当③∠A=∠C,④∠B=∠D时,四边形ABCD为平行四边形;
故选:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果x+y=1,x2+y2=3,那么x3+y3= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2+mx+1=0根的判别式的值为5,则m=( )
A. ±3B. 3C. 1D. ±1
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A. 3x2y﹣2x2y=x2y B. 5y﹣3y=2 C. 3a+2b=5ab D. 7a+a=7a2
-
科目: 来源: 题型:
查看答案和解析>>【题目】x,y表示两个数,规定新运算“※”及“△”如下:x※y=6x+5y,x△y=3xy,则(﹣2※3)△(﹣4)=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程:
(1)(x﹣5)2=8(x﹣5)
(2)2x2﹣4x﹣3=0. -
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读第(1)题的解答过程,然后再解第(2)题.
(1)已知多项式2x3﹣x2+m有一个因式是2x+1,求m的值.
解法一:设2x3﹣x2+m=(2x+1)(x2+ax+b),
则:2x3﹣x2+m=2x3+(2a+1)x2+(a+2b)x+b
比较系数得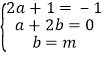 , 解得
, 解得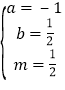 , ∴
, ∴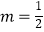
解法二:设2x3﹣x2+m=A(2x+1)(A为整式)
由于上式为恒等式,为方便计算了取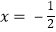 ,
,
2× =0,故
=0,故 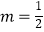 .
.
(2)已知x4+mx3+nx﹣16有因式(x﹣1)和(x﹣2),求m、n的值.
相关试题

