【题目】如图,将![]() 沿过点
沿过点![]() 的直线
的直线![]() 折叠,使点
折叠,使点![]() 落到
落到![]() 边上的
边上的![]() 处,折痕交
处,折痕交![]() 边于点
边于点![]() ,连接
,连接![]() .
.
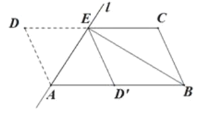
(1)求证:四边形![]() 是平行四边形;
是平行四边形;
(2)若![]() 平分
平分![]() ,求证:
,求证:![]() .
.
参考答案:
【答案】(1)详见解析;(2)详见解析.
【解析】
(1)利用翻折变换的性质以及平行线的性质得出∠DAE=∠EAD′=∠DEA=∠D′EA,进而利用平行四边形的判定方法得出四边形DAD′E是平行四边形,进而求出四边形BCED′是平行四边形;
(2)利用平行线的性质结合勾股定理得出答案.
(1)∵将ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,
∴∠DAE=∠D′AE,∠DEA=∠D′EA,∠D=∠AD′E,
∵DE∥AD′,
∴∠DEA=∠EAD′,
∴∠DAE=∠EAD′=∠DEA=∠D′EA,
∴∠DAD′=∠DED′,
∴四边形DAD′E是平行四边形,
∴DE=AD′,
∵四边形ABCD是平行四边形,
∴AB∥DC,
∴CE ∥D′B,
∴四边形BCED′是平行四边形;
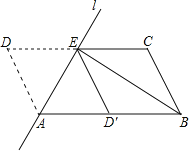
(2)∵BE平分∠ABC,
∴∠CBE=∠EBA,
∵AD∥BC,
∴∠DAB+∠CBA=180°,
∵∠DAE=∠BAE,
∴∠EAB+∠EBA=90°,
∴∠AEB=90°,
∴AB2=AE2+BE2.
-
科目: 来源: 题型:
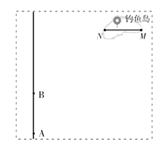
查看答案和解析>>【题目】钓鱼岛自古就是中国的领土,我国有 关部门已对钓鱼岛及其附属岛屿开展常态化监视监测. M、N 为钓鱼岛上东西海岸线上的两点,MN 之间的距 离约为3.6km. 某日,我国一艘海监船从 A 点沿正北方 向巡航,在 A 点测得岛屿的西端点 N 在点 A 的北偏东350方向;海监船继续航行 4km 后到达 B 点 ,测得岛屿的东端点 M 在点 B 的北偏东 600方向,求点 M 距离海监船航线的最短距离 (结果精确到 0.1km).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某文化用品商店用1 000元购进一批“晨光”套尺,很快销售一空;商店又用1 500元购进第二批该款套尺,购进时单价是第一批的
 倍,所购数量比第一批多100套.
倍,所购数量比第一批多100套.(1)求第一批套尺购进时单价是多少?
(2)若商店以每套4元的价格将这两批套尺全部售出,可以盈利多少元?
-
科目: 来源: 题型:
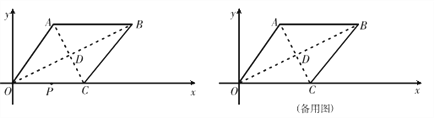
查看答案和解析>>【题目】如图,在菱形 OA BC 中,已知点 B(8,4),C(5,0),
点 D 为 OB、AC 交点,点 P 从原点出发向 x 轴正方向运动;
(1) 在点 P 运动过程中,若∠OBP=900,求出点 P 坐标;
(2) 在点 P 运动过程中,若∠PDC+∠BCP=900,求出点 P 坐标;
(3) 点 P 在(2)的位置时停止运动,点 M 从点 P 出发沿 x 轴正方向运动,连结 BM,若点 P 关于BM 的对称点 P’到 AB 所在直线的距离为 2,求此时点 M 的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某水果店经销进价分别为
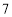 元/千克、
元/千克、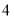 元/千克的甲、乙两种水果,下表是近两天的销售情况:(进价、售价均保持不变,利润=售价-进价)
元/千克的甲、乙两种水果,下表是近两天的销售情况:(进价、售价均保持不变,利润=售价-进价)时间
甲水果销量
乙水果销量
销售收入
周五
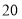 千克
千克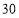 千克
千克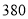 元
元周六
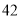 千克
千克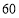 千克
千克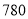 元
元(1)求甲、乙两种水果的销售单价;
(2)若水果店准备用不多于
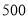 元的资金再购进两种水果共
元的资金再购进两种水果共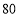 千克,求最多能够进甲水果多少千克?
千克,求最多能够进甲水果多少千克?(3)在(2)的条件下,水果店销售完这
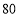 千克水果能否实现利润为
千克水果能否实现利润为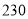 元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
元的目标?若能,请给出相应的采购方案;若不能,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
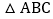 中,
中,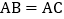 ,D在边AC上,且
,D在边AC上,且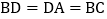 .
. 如图1,填空
如图1,填空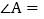 ______
______ ,
,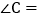 ______
______
 如图2,若M为线段AC上的点,过M作直线
如图2,若M为线段AC上的点,过M作直线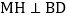 于H,分别交直线AB、BC与点N、E.
于H,分别交直线AB、BC与点N、E. 求证:
求证: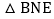 是等腰三角形;
是等腰三角形; 试写出线段AN、CE、CD之间的数量关系,并加以证明.
试写出线段AN、CE、CD之间的数量关系,并加以证明.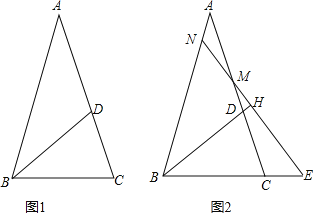
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图 ,在平面直角坐标系中 ,已知二次函数y=ax2+bx+c (a≠0)
的图象经过 A(-1,0),B(3,0),C(6,4)三点.
(1)求此二次函数解析式和顶点 D 的坐标;
(2)①E为抛物线对称轴上一点,过点E作FG//x 轴,分别交抛物线于F、G两点 ,若
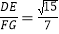 ,求点E的坐标;
,求点E的坐标;② 若抛物线对称轴上点 H 到直线 BC 的距离等于点 H 到 x 轴的距离,则求出点 H
的坐标;
(3)在(2)的条件下,以点I(1,
 )为圆心,IH 的长为半径作⊙I,J 为⊙I上的动点,求是否存在一个定值
)为圆心,IH 的长为半径作⊙I,J 为⊙I上的动点,求是否存在一个定值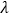 ,使得 CJ+
,使得 CJ+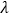 EJ 的最小值是
EJ 的最小值是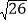 若不存在,请说明理由.若存在,请求出
若不存在,请说明理由.若存在,请求出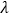 的值;
的值;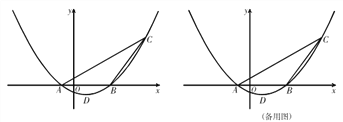
相关试题

