Question

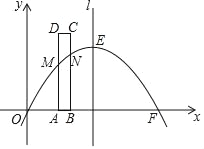
【题目】如图，已知抛物线y=ax2+bx与x轴分别交于原点O和点F（10，0），与对称轴l交于点E（5，5）．矩形ABCD的边AB在x轴正半轴上，且AB=1，边AD，BC与抛物线分别交于点M，N．当矩形ABCD沿x轴正方向平移，点M，N位于对称轴l的同侧时，连接MN，此时，四边形ABNM的面积记为S；点M，N位于对称轴l的两侧时，连接EM，EN，此时五边形ABNEM的面积记为S．将点A与点O重合的位置作为矩形ABCD平移的起点，设矩形ABCD平移的长度为t（0≤t≤5）．

（1）求出这条抛物线的表达式；

（2）当t=0时，求S△OBN的值；

（3）当矩形ABCD沿着x轴的正方向平移时，求S关于t（0＜t≤5）的函数表达式，并求出t为何值时，S有最大值，最大值是多少？

Answer 1

【答案】（1）抛物线的表达式为y=﹣x2+2x；（2）；

（3）S=﹣（t﹣）2+（0＜t≤4）；S＝﹣（t﹣）2+（4＜t≤5），当t=时，S有最大值，最大值是.

【解析】

（1）将E（5，5）、F（10，0）代入y=ax2+bx，求解即可得到答案；

（2）当t=0时，点B的坐标为（1，0），点N的坐标为（1，），然后根据三角形的面积公式计算即可；

（3）①当0＜t≤4时（图1），S为梯形ABNM的面积，用t表示出各点的坐标，然后根据梯形面积公式得到关于t的二次函数，再利用二次函数的性质求得S的最大值；

②当4＜t≤5时（图2），S为五边形ABNEM的面积，即两个梯形相加，同①求得S的最大值，与①所得S进行比较，较大的即为所求.

（1）将E（5，5）、F（10，0）代入y=ax2+bx，

，

解得：，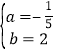

∴抛物线的表达式为y=﹣x2+2x；

（2）当t=0时，点B的坐标为（1，0），点N的坐标为（1，），

∴BN=，OB=1，

∴S△OBN=BNOB=；

（3）①当0＜t≤4时（图1），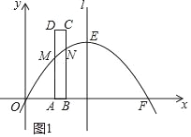

点A的坐标为（t，0），点B的坐标为（t+1，0），

∴点M的坐标为（t，﹣t2+2），点N的坐标为（t+1，﹣（t+1）2+2（t+1）），

∴AM=﹣t2+2t，BN=﹣（t+1）2+2（t+1），

∴S=（AM+BN）AB=×1×[﹣t2+2t﹣（t+1）2+2（t+1）]，

=﹣t2+t+，

=﹣（t﹣）2+，

∵﹣＜0，

∴当t=4时，S取最大值，最大值为；

②当4＜t≤5时（图2），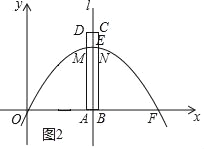

点A的坐标为（t，0），点B的坐标为（t+1，0），

∴点M的坐标为（t，﹣t2+2t），点N的坐标为（t+1，﹣（t+1）2+2（t+1）），

∴AM=﹣t2+2t，BN=﹣（t+1）2+2（t+1），

∴S=（5﹣t）（﹣t2+2t+5）+（t﹣4）[5﹣（t+1）2+2（t+1）]，

=（t3﹣3t2+5t+25）+（﹣t3+t2+t﹣），

=﹣t2+t﹣，

=﹣（t﹣）2+，

∵﹣＜0，

∴当t=时，S取最大值，最大值为；

∵=＜，

∴当t=时，S有最大值，最大值是．