搜索
【题目】为了帮助某地区重建家园，某班全体学生积极捐款，捐款金额共2600元，其中18名女生人均捐款a元，则该班男生共捐款元．（用含有a的代数式表示）
参考答案：
【答案】（2600﹣18a）
【解析】解：由题意得：18名女生共捐款18a元，
则该班男生共捐款（2600﹣18a）元．
所以答案是：（2600﹣18a）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】【问题情境】：
如图1，AB//CD，∠PAB=130°，∠PCD=120°，求∠APC的度数．
小明的思路是：过P作PE//AB，通过平行线性质来求∠APC．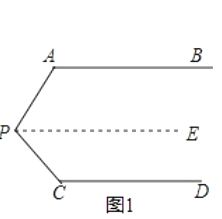
（1）按小明的思路，求∠APC的度数；
（2）【问题迁移】：
如图2，AB//CD，点P在射线OM上运动，记∠PAB=α，∠PCD=β，当点P在B、D两点之间运动时，问∠APC与α、β之间有何数量关系？请说明理由；
（3）【问题应用】：
在（2）的条件下，如果点P在B、D两点外侧运动时（点P与点O、B、D三点不重合），请直接写出∠APC与α、β之间的数量关系． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AB=c，AC=b．AD是△ABC的角平分线，DE⊥A于E，DF⊥AC于F，EF与AD相交于O，已知△ADC的面积为1．
（1）证明：DE=DF；
（2）试探究线段EF和AD是否垂直？并说明理由；
（3）若△BDE的面积是△CDF的面积2倍．试求四边形AEDF的面积．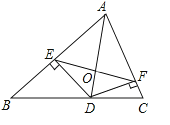
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△AOB中，A（－8，0），B（0，
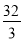），AC平分∠OAB，交y轴于点C，点P是x轴上一点，⊙P经过点A、C，与x轴于点D，过点C作CE⊥AB，垂足为E，EC的延长线交x轴于点F，（1）⊙P的半径为 ；
（2）求证：EF为⊙P的切线；
（3）若点H是
上一动点，连接OH、FH，当点H在
上运动时，试探究
是否为定值？若为定值，求其值；若不是定值，请说明理由.
-
科目： 来源： 题型：
查看答案和解析>>【题目】完成下面推理过程：
如图，已知∠1=∠2，∠B=∠C，可推得AB//CD．理由如下：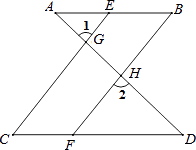
∵∠1=∠2 ，
且∠1=∠CGD ，
∴∠2=∠CG ，
∴CE//BF ，
∴∠=∠C两直线平行，同位角相等；
又∵∠B=∠C（已知），
∴∠BFD=∠B，
∴AB//CD ． -
科目： 来源： 题型：
查看答案和解析>>【题目】为了了解某校300名初三学生的睡眠时间，从中抽取30名学生进行调查，在这个问题中，下列说法正确的是 ( )
A. 300名学生是总体 B. 300是众数
C. 30名学生是抽取的一个样本 D. 30是样本的容量
-
科目： 来源： 题型：
查看答案和解析>>【题目】用配方法解方程2x2-4x=3时，先把二次项系数化为1，然后方程的两边都应加上_____________.
相关试题
