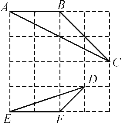
【题目】如图,在4×4的正方形网格中,△ABC和△DEF的顶点都在边长为1的正方形的顶点上.
(1)填空:∠ABC=__________度,BC=_________;
(2)求证:∠C=∠E.
参考答案:
【答案】(1) 135°,2![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)根据正方形的对角线可得∠ABC的补角等于45°,即可求出∠ABC=135°,根据BC是正方形的对角线,利用勾股定理进行计算即可.
(2)先根据勾股定理计算出网格中三角形的各个边长,然后求出各边比值,根据三边对应成比例两三角形相似可得△ABD∽△DCB,然后再可得
(1) 135° 2![]()
(2) 由图知,AB=2,BC=2![]() ,AC=2
,AC=2![]() ,DF=
,DF=![]() ,EF=2,DE=
,EF=2,DE=![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴△DEF∽△ACB,
∴∠C=∠E.
-
科目: 来源: 题型:
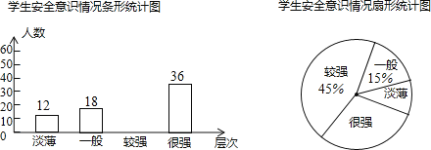
查看答案和解析>>【题目】某校为了解学生的安全意识情况,在全校范围内随机抽取部分学生进行问卷调查,根据调查结果,把学生的安全意识分成“淡薄”、“一般”、“较强”、“很强”四个层次,并绘制成如图9的两幅尚不完整的统计图.
根据以上信息,解答下列问题:
(1)这次调查一共抽取了 名学生;
(2)请将条形统计图补充完整;
(3)分别求出安全意识为“淡薄”的学生占被调查学生总数的百分比、安全意识为“很强”的学生所在扇形的圆心角的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个铝质的三角形框架的三边长分别为24 cm,30 cm,36 cm,要做一个与它相似的铝质三角形的框架,现有长27 cm,45 cm的两根铝材,要求以其中的一根为边,从另一根上截下两段(允许有余材),则截法有______种.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两个等腰直角△ABC和△CDE中,∠ACB=∠DCE=90°.
(1)观察猜想如图1,点E在BC上,线段AE与BD的数量关系,位置关系.
(2)探究证明把△CDE绕直角顶点C旋转到图2的位置,(1)中的结论还成立吗?说明理由;
(3)拓展延伸:把△CDE绕点C在平面内自由旋转,若AC=BC=13,DE=10,当A、E、D三点在直线上时,请直接写出AD的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是上海世博园内的一个矩形花园,花园长为100米,宽为50米,在它的四角各建有一个同样大小的正方形观光休息亭,四周建有与观光休息亭等宽的观光大道,其余部分(图中阴影部分)种植的是不同花草.已知种植花草部分的面积为3600米2,那么矩形花园各角处的正方形观光休息亭的边长为多少米?

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=3,连接DE.
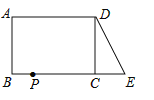
(1)DE的长为 .
(2)动点P从点B出发,以每秒1个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P运动的时间为t秒,求当t为何值时,△ABP和△DCE全等?
(3)若动点P从点B出发,以每秒1个单位的速度仅沿着BE向终点E运动,连接DP.设点P运动的时间为t秒,是否存在t,使△PDE为等腰三角形?若存在,请直接写出t的值;否则,说明理由.
-
科目: 来源: 题型:
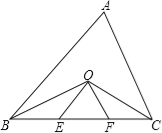
查看答案和解析>>【题目】已知如图,BC=3,∠ABC和∠ACB的平分线相交于点O,OE∥AB,OF∥AC,则三角形OEF的周长为 .
相关试题

