【题目】数学是一门充满乐趣的学科,某校七年级小凯同学的数学学习小组遇到一个富有挑战性的探究问题,请你帮助他们完成整个探究过程;
(问题背景)
对于一个正整数![]() ,我们进行如下操作:
,我们进行如下操作:
(1)将![]() 拆分为两个正整数
拆分为两个正整数![]() ,
,![]() 的和,并计算乘积
的和,并计算乘积![]() ;
;
(2)对于正整数![]() ,
,![]() ,分别重复此操作,得到另外两个乘积;
,分别重复此操作,得到另外两个乘积;
(3)重复上述过程,直至不能再拆分为止,(即拆分到正整数1);
(4)将所有的乘积求和,并将所得的数值称为该正整数的“神秘值”,请探究不同的拆分方式是否影响正整数![]() 的“神秘值”,并说明理由.
的“神秘值”,并说明理由.
(尝试探究):
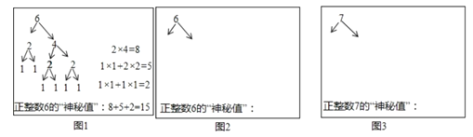
(1)正整数2的“神秘值”是_________;
(2)为了研究一般的规律,小凯所在学习小组通过讨论,决定再选择两个具体的正整数6和7,重复上述过程
探究结论:
如图1所示,是小凯选择的一种拆分方式,通过该拆分方法得到正整数6的“神秘值”为15.
请模仿小凯的计算方式,在图2中,选择另外一种拆分方式,给出计算正整数6的“神秘值”的过程;对于正整数7,请选择一种拆分方式,在图3中给出计算正整数7的“神秘值”的过程.
(结论猜想)
结合上面的实践活动,进行更多的尝试后,小凯所在学习小组猜测,正整数![]() 的“神秘值”与其拆分方法无关.请帮助小凯,利用尝试成果,猜想正整数
的“神秘值”与其拆分方法无关.请帮助小凯,利用尝试成果,猜想正整数![]() 的“神秘值”的表达式为________.(用含字母
的“神秘值”的表达式为________.(用含字母![]() 的代数式表示,直接写出结果)
的代数式表示,直接写出结果)
参考答案:
【答案】尝试探究:(1)1;(2)见解析;结论猜想:![]()
【解析】
尝试探究:(1)根据神秘值的定义,将正整值分解,求和即可;
(2)将6和7分解,直到不能分解位置,再将所有的乘积求和即可;
结论猜想:找出多个值的神秘值,再找出规律即可.
解:尝试探究:(1)∵2可以分为1和1,
∴2的神秘值是1,
(2)如图,
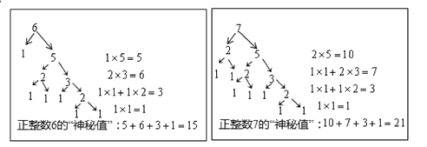
结论猜想:∵2的神秘值是1,3的神秘值是3,4的神秘值是6,5的神秘值是10,6的神秘值是15,7的神秘值是21,…,
∴正整值n(n>1)的“神秘值”为n与n-1之积的一半,
即n的神秘值是![]() (n>1).
(n>1).
故答案为正整值n(n>1)的“神秘值”为n与n-1之积的一半;![]() (n>1).
(n>1).
-
科目: 来源: 题型:
查看答案和解析>>【题目】定理描述
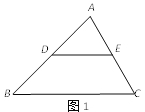
(1)如图1,用文字语言或符号语言叙述三角形中位线性质定理的内容.
.
证法回顾
证明三角形中位线性质定理的方法很多,但多数都需要通过添加辅助线构图去完成.下列是其中一种证法的添加辅助线方法:
添加辅助线,如图2,在△ABC中,过点C作CF∥AB,与DE的延长线交于点F.
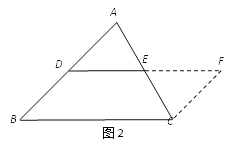
(2)上述证法中,证明三角形中位线定理中的DE∥BC的依据是( )
A.同位角相等,两直线平行.
B.平行四边形对边平行.
C.同旁内角互补,两直线平行.
D.平行于同一条直线的两条直线互相平行
拓展延伸
(3)利用证明三角形中位线定理获得的经验解决下面的问题:
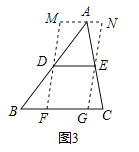
如图3,在△ABC中,∠B=45°,AB=10,BC=8,DE是△ABC的中位线,过点D、E作DF∥EG,分别交BC于F、G,过点A作MN∥BC,分别与FD、GE的延长线交于M、N,则四边形MFGN周长的最小值是
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD中,对角线AC、BD相交于点O,给出下列四组条件:①AB∥CD,AD∥BC;②AB=CD,AD=BC;③AO=CO,BO=DO;④AB∥CD,AD=BC。其中一定能判断这个四边形是平行四边形的条件共有
A. 1组 B. 2组 C. 3组 D. 4组
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一只甲虫在
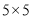 的方格(每小格边长为1)上沿着网格线运动,他从
的方格(每小格边长为1)上沿着网格线运动,他从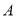 处出发去看望
处出发去看望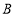 、
、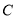 、
、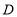 处的其他甲虫,规定:向上向右走均为正,向下向左走均为负,如果从
处的其他甲虫,规定:向上向右走均为正,向下向左走均为负,如果从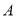 到
到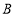 记为
记为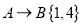 ,从
,从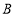 到
到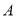 记为:
记为: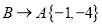 ,其中第一个数表示左右方向,第二个数表示上下方向.
,其中第一个数表示左右方向,第二个数表示上下方向.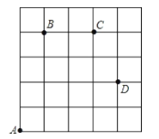
(1)图中
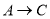 {_______,_________},
{_______,_________},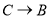 {_______,_________};
{_______,_________};(2)若这只甲虫的行走路线为
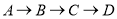 ,请计算该甲虫走过的最短路程.
,请计算该甲虫走过的最短路程.(3)若图中另有两个格点
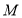 、
、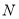 ,且
,且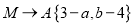 ,
,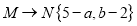 ,则
,则 应记为什么?直接写出你的答案.
应记为什么?直接写出你的答案. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE、BF相交于点O,下面四个结论:(1)AE=BF,(2)AE⊥BF,(3)AO=OE,(4)S△AOB=S四边形DEOF,其中正确结论的序号是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一条笔直公路BD的正上方A处有一探测仪,AD=24m,∠D=90°,一辆轿车从B点匀速向D点行驶,测得∠ABD=31°,2秒后到达C点,测得∠ACD=50°.
(Ⅰ)求B,C两点间的距离(结果精确到1m);
(Ⅱ)若规定该路段的速度不得超过15m/s,判断此轿车是否超速.
参考数据:tan31°≈0.6,tan50°≈1.2.

-
科目: 来源: 题型:
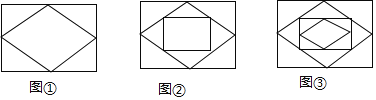
查看答案和解析>>【题目】已知:顺次连接矩形各边的中点,得到一个菱形,如图①;再顺次连接菱形各边的中点,得到一个新的矩形.如图②;然后顺次连接新的矩形各边的中点,得到一个新的菱形,如图③;如此反复操作下去,则第3个图形中直角三角形的个数有______个,第2018个图形中直角三角形的个数有______个.
相关试题

