【题目】自行车厂某周计划生产2100辆电动车,平均每天生产电动车300辆.由于各种原因,实际每天的生产量与计划每天的生产量相比有出入,下表是该周的实际生产情况(超产记为正、减产记为负,单位:辆):
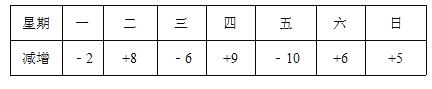
(1)该厂星期一生产电动车 辆;
(2)生产量最多的一天比生产量最少的一天多生产电动车 辆;
(3)该厂实行记件工资制,每生产一辆车可得60元,那么该厂工人这一周的工资总额是多少元?
参考答案:
【答案】(1)298;(2)19;(3)该厂工人这一周的工资总额是126600元.
【解析】
(1)根据题意用计划平均每天生产量加上减产数即可.
(2)根据表中数据,生产量最多的一天为300+9=309辆,最少的一天为300﹣10=290辆,前者减去后者即可.
(3)直接将图表中所有数据相加可得一周以来生产量超减产数,加上计划生产数,再乘以单件工资即可解决.
解:(1)∵每天平均300辆,超产记为正、减产记为负,∴周一生产电车为300﹣2=298;
(2)∵生产量最多的一天为300+9=309辆,生产量最少的一天为300﹣10=290辆,309-290=19辆
∴生产量最多的一天比生产量最少的一天多生产电动车19辆;
(3)一周总共生产电车为7×300+(﹣2+8﹣6+9﹣10+6+5)=2110辆,
∴该厂工人这一周的工资总额是60×2110=126600元.
答:该厂工人这一周的工资总额是126600元.
故答案为:298,19, 126600.
-
科目: 来源: 题型:
查看答案和解析>>【题目】矩形ABCD中,AB=6,BC=8.点P在矩形ABCD的内部,点E在边BC上,满足△PBE∽△DBC,若△APD是等腰三角形,则PE的长为数___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在由边长为1个单位长度的小正方形组成的10×10网格中,已知点O,A,B均为网格线的交点.
(1)在给定的网格中,以点O为位似中心,将线段AB放大为原来的2倍,得到线段
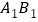 (点A,B的对应点分别为
(点A,B的对应点分别为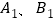 ).画出线段
).画出线段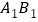 ;
;(2)将线段
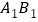 绕点
绕点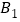 逆时针旋转90°得到线段
逆时针旋转90°得到线段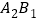 .画出线段
.画出线段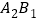 ;
;(3)以
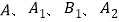 为顶点的四边形
为顶点的四边形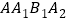 的面积是 个平方单位.
的面积是 个平方单位.
-
科目: 来源: 题型:
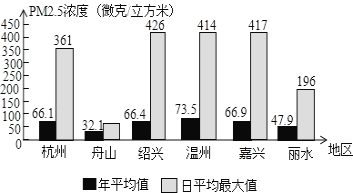
查看答案和解析>>【题目】2017年1月10日,绿色和平发布了全国74个城市PM2.5浓度年均值排名和相应的最大日均值,其中浙江省六个地区的浓度如下图所示(舟山的最大日均值条形图缺损)以下说法中错误的是______.
①则六个地区中,最大日均值最高的是绍兴;②杭州的年均值大约是舟山的2倍;③舟山的最大日均值不一定低于丽水的最大日均值;④六个地区中,低于国家环境空气质量标准规定的年均值35微克每立方米的地区只有舟山.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了测量竖直旗杆AB的高度,某综合实践小组在地面D处竖直放置标杆CD,并在地面上水平放置个平面镜E,使得B,E,D在同一水平线上,如图所示.该小组在标杆的F处通过平面镜E恰好观测到旗杆顶A(此时∠AEB=∠FED).在F处测得旗杆顶A的仰角为39.3°,平面镜E的俯角为45°,FD=1.8米,问旗杆AB的高度约为多少米? (结果保留整数)(参考数据:tan39.3°≈0.82,tan84.3°≈10.02)

-
科目: 来源: 题型:
查看答案和解析>>【题目】学完《平面直角坐标系》和《一次函数》这两章后,老师布置了这样一道思考题:已知:如图,在长方形
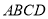 中,
中,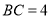 ,
,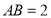 ,点
,点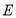 为
为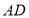 的中点,
的中点,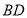 和
和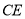 相交于点
相交于点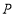 .求
.求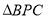 的面积.小明同学应用所学知识,顺利地解决了此题,他的思路是这样的:以
的面积.小明同学应用所学知识,顺利地解决了此题,他的思路是这样的:以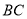 所在的直线为
所在的直线为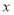 轴,以
轴,以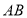 所在的直线为
所在的直线为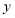 轴建立适当的平面直角坐标系,写出图中一些点坐标.根据一次函数的知识求出点
轴建立适当的平面直角坐标系,写出图中一些点坐标.根据一次函数的知识求出点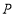 的坐标,从而求得
的坐标,从而求得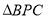 的面积.请你按照小明的思路解决这道思考题.
的面积.请你按照小明的思路解决这道思考题.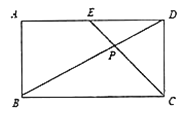
-
科目: 来源: 题型:
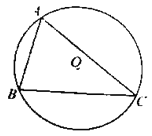
查看答案和解析>>【题目】如图,⊙O为锐角△ABC的外接圆,半径为5.
(1)用尺规作图作出∠BAC的平分线,并标出它与劣弧BC的交点E(保留作图痕迹,不写作法);
(2)若(1)中的点E到弦BC的距离为3,求弦CE的长.
相关试题

