【题目】如图①,直线PQ同侧有两点M,N,点T在直线PQ上,若∠MTP=∠NTQ,则称点T为M,N在直线PQ上的投射点.
(1)如图②,在Rt△ABC中,∠B=60°,D为斜边AB的中点,E为AC的中点.求证:点D为C,E在直线AB上的投射点;
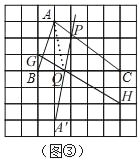
(2)如图③,在正方形网格中,已知点A,B,C三点均在格点上,请仅用没有刻度的直尺在AC上画出点P,在BC上画出点Q,使A,P在BC上的投射点Q满足CQ=2BQ;
(3)如图④,在Rt△ABC中,∠C=90°,AC=BC,在AB,BC边上是否分别存在点D,E,使点D为E,C在AB上的投射点,点E为A,D在BC上的投射点?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
参考答案:
【答案】(1)证明见解析;(2)画图见解析;(3)存在,![]() .
.
【解析】
(1)先求出∠BDC=60°,进而判断出∠ADE=∠B=60°,即可得出结论;
(2)根据对称性即可作出图形;
(3)根据对称和相似作出图形,再用相似三角形的性质即可得出结论.
(1)∵在Rt△ABC中,D为斜边AB的中点,
∴CD=BD=![]() BC,
BC,
又∵∠B=60°,
∴∠BDC=60°,
∵D,E分别为AB,AC的中点,
∴DE∥AC,
∴∠ADE=∠B=60°,
∴∠ADE=∠BDC,
∴点D为C,E在直线AB上的投射点;
(2)如图③,
作法:
1、在格点上取点G,H,连接HG交BC于Q,(理由:△BQG∽△HQC)
2、作点A关于BC的对称点A',连接A'Q并延长交AC于P,(∠AQB=∠A'QB=∠PQC)
即:点P就是所求作的点;
(3)存在,
如图④,作点C关于AB的对称点C′,连接BC',AC',
则四边形ACBC′为正方形,
作点A关于BC的对称点A′,连接A'C'交AB于D,交BC于E,
即:点D,E是所求作的点,
∴C′,D,E,A在同一直线上,
CA′=CA=C′A=C′B=BC,CD=C′D,
∴△C′BE≌△A′CE,
∴BE=![]() BC=
BC=![]() C′A,
C′A,
∵AC′∥BC,
∴△BDE∽△ADC′,
∴![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
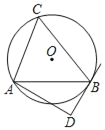
查看答案和解析>>【题目】如图,⊙O的半径为5,△ABC是⊙O的内接三角形,AB=8.AD和过点B的切线互相垂直,垂足为D.
(1)求证:∠BAD+∠C=90°;
(2)求线段AD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】A厂一月份产值为16万元,因管理不善,二、三月份产值的月平均下降率为x(0<x<1).B厂一月份产值为12万元,二月份产值下降率为x,经过技术革新,三月份产值增长,增长率为2x.三月份A、B两厂产值分别为yA、yB(单位:万元).
(1)分别写出yA、yB与x的函数表达式;
(2)当yA=yB时,求x的值;
(3)当x为何值时,三月份A、B两厂产值的差距最大?最大值是多少万元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=﹣x2+2kx﹣k2+k+3(k为常数)的顶点纵坐标为4.
(1)求k的值;
(2)设抛物线与直线y=﹣
 (x﹣3)(m≠0)两交点的横坐标为x1,x2,n=x1+x2﹣2,若A(1,a),B(b,
(x﹣3)(m≠0)两交点的横坐标为x1,x2,n=x1+x2﹣2,若A(1,a),B(b, )两点在动点M(m,n)所形成的曲线上,求直线AB的解析式;
)两点在动点M(m,n)所形成的曲线上,求直线AB的解析式;(3)将(2)中的直线AB绕点(3,0)顺时针旋转45°,与抛物线x轴上方的部分相交于点C,请直接写出点C的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直角三角形的直角顶点在坐标原点,∠OAB=30°,若点A在反比例函数y=
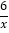 (x>0)的图象上,则经过点B的反比例函数解析式为( )
(x>0)的图象上,则经过点B的反比例函数解析式为( )
A. y=﹣
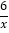 B. y=﹣
B. y=﹣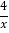 C. y=﹣
C. y=﹣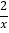 D. y=
D. y=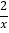
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,∠ABC=120°,将菱形折叠,使点A恰好落在对角线BD上的点G处(不与B、D重合),折痕为EF,若DG=2,BG=6,则BE的长为______.
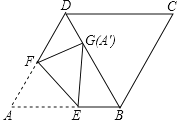
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明统计了某校八年级(3)班五位同学每周课外阅读的平均时间,其中四位同学每周课外阅读时间分别是
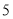 小时、
小时、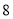 小时、
小时、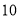 小时、
小时、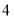 小时,第五位同学每周的课外阅读时间既是这五位同学每周课外阅读时间的中位数,又是众数,则第五位同学每周课外阅读时间是( )
小时,第五位同学每周的课外阅读时间既是这五位同学每周课外阅读时间的中位数,又是众数,则第五位同学每周课外阅读时间是( )A.
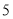 小时B.
小时B.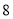 小时C.
小时C.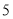 或
或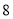 小时D.
小时D.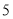 或
或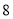 或
或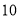 小时
小时
相关试题

