【题目】如图,反比例函数y1=![]() 与一次函数y2=kx+b的图象交于两点A(n,﹣1)、B(1,2).
与一次函数y2=kx+b的图象交于两点A(n,﹣1)、B(1,2).
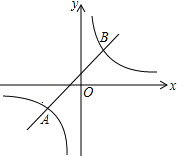
(1)求反比例函数与一次函数的关系式;
(2)根据图象,直接回答:当x取何值时,y1≥y2?
(3)连接OA、OB,求△AOB的面积.
参考答案:
【答案】见解析
【解析】
试题分析:(1)先把A代入反比例函数解析式,求得m的值,进而求得n的值,把A,B两点分别代入一次函数解析式即可.
(2)根据图象,结合交点坐标即可求得;
(3)求出直线与x轴的交点坐标,将△ABO的面积分成两个三角形的面积来求即可.
解:(1)∵B(1,2).在反比例函数y1=![]() 上,
上,
∴m=2,
∴反比例函数解析式为y1=![]() ;
;
又∵点A(n,﹣1)在y1=![]() 上,
上,
∴n=﹣2,
∴点B的坐标为(﹣2,﹣1),
把A(1,2)和B(﹣2,﹣1)两点的坐标代入一次函数y2=kx+b得![]() ,
,
解得![]() .
.
∴一次函数的解析为y=x+1.
(2)∵A(1,2),B(﹣2,﹣1),
∴当﹣2≤x<0或x≥1时,y1≥y2;
(3)∵一次函数的解析式为y=x+1,
令y=0得:x+1=0,即x=﹣1,
∴S△ABO=![]() ×1×1+
×1×1+![]() ×1×2=1.5.
×1×2=1.5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若ABCD的三条边分别为8cm,(x﹣2)cm,(x+3)cm,则该ABCD的周长是cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P(3,4)关于y轴对称的点的坐标是( )
A. (3,﹣4)B. (﹣3,4)C. (﹣4,﹣3)D. (﹣4,3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=8cm,AB=10cm.点P从点A出发,以5cm/s的速度从点A运动到终点B;同时,点Q从点C出发,以3cm/s的速度从点C运动到终点B,连结PQ;过点P作PD⊥AC交AC于点D,将△APD沿PD翻折得到△A′PD,以A′P和PB为邻边作A′PBE,A′E交射线BC于点F,交射线PQ于点G.设A′PBE与四边形PDCQ重叠部分图形的面积为Scm2,点P的运动时间为ts.
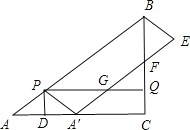
(1)当t为 时,点A′与点C重合;
(2)求S与t的函数关系式;
(3)请直接写出当射线PQ将A′PBE分成的两部分图形的面积之比是1:3时t的值.
-
科目: 来源: 题型:
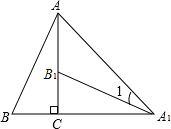
查看答案和解析>>【题目】如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A1B1C,连结AA1,若∠AA1B1=15°,则∠B的度数是 .
-
科目: 来源: 题型:
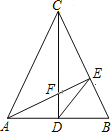
查看答案和解析>>【题目】△ABC中,CA=CB,CD是中线,AE⊥BC于E交CD于F,求证:①△CBD∽△AFD,②DE2=DFDC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的顶点B,C在x轴的正半轴上,反比例函数y=
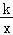 (k≠0)在第一象限的图象经过顶点A(m,2)和CD边上的点E(n,
(k≠0)在第一象限的图象经过顶点A(m,2)和CD边上的点E(n, ),过点E的直线l交x轴于点F,交y轴于点G(0,﹣2),则点F的坐标是( )
),过点E的直线l交x轴于点F,交y轴于点G(0,﹣2),则点F的坐标是( )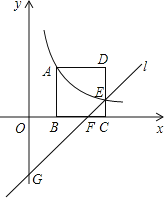
A.(
 ,0) B.(
,0) B.( ,0) C.(
,0) C.( ,0) D.(
,0) D.( ,0)
,0)
相关试题

