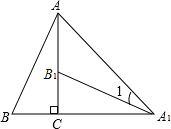
【题目】如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A1B1C,连结AA1,若∠AA1B1=15°,则∠B的度数是 .
参考答案:
【答案】60°
【解析】
试题分析:根据旋转的性质可得AC=A1C,然后判断出△ACA1是等腰直角三角形,根据等腰直角三角形的性质可得∠CAA1=45°,再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠A1B1C,然后根据旋转的性质可得∠B=∠A1B1C.
解:∵Rt△ABC绕直角顶点C顺时针旋转90°得到△A1B1C,
∴AC=A1C,
∴△ACA1是等腰直角三角形,
∴∠CAA1=15°,
∴∠A1B1C=∠1+∠CAA1=15°+45°=60°,
由旋转的性质得∠B=∠A1B1C=60°,
故答案为60°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P(3,4)关于y轴对称的点的坐标是( )
A. (3,﹣4)B. (﹣3,4)C. (﹣4,﹣3)D. (﹣4,3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=8cm,AB=10cm.点P从点A出发,以5cm/s的速度从点A运动到终点B;同时,点Q从点C出发,以3cm/s的速度从点C运动到终点B,连结PQ;过点P作PD⊥AC交AC于点D,将△APD沿PD翻折得到△A′PD,以A′P和PB为邻边作A′PBE,A′E交射线BC于点F,交射线PQ于点G.设A′PBE与四边形PDCQ重叠部分图形的面积为Scm2,点P的运动时间为ts.
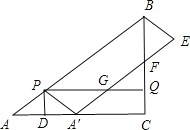
(1)当t为 时,点A′与点C重合;
(2)求S与t的函数关系式;
(3)请直接写出当射线PQ将A′PBE分成的两部分图形的面积之比是1:3时t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反比例函数y1=
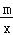 与一次函数y2=kx+b的图象交于两点A(n,﹣1)、B(1,2).
与一次函数y2=kx+b的图象交于两点A(n,﹣1)、B(1,2).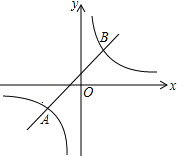
(1)求反比例函数与一次函数的关系式;
(2)根据图象,直接回答:当x取何值时,y1≥y2?
(3)连接OA、OB,求△AOB的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,CA=CB,CD是中线,AE⊥BC于E交CD于F,求证:①△CBD∽△AFD,②DE2=DFDC.
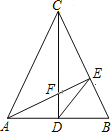
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的顶点B,C在x轴的正半轴上,反比例函数y=
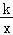 (k≠0)在第一象限的图象经过顶点A(m,2)和CD边上的点E(n,
(k≠0)在第一象限的图象经过顶点A(m,2)和CD边上的点E(n, ),过点E的直线l交x轴于点F,交y轴于点G(0,﹣2),则点F的坐标是( )
),过点E的直线l交x轴于点F,交y轴于点G(0,﹣2),则点F的坐标是( )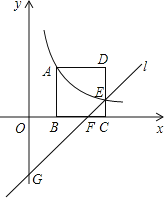
A.(
 ,0) B.(
,0) B.( ,0) C.(
,0) C.( ,0) D.(
,0) D.( ,0)
,0) -
科目: 来源: 题型:
查看答案和解析>>【题目】计算 (x+2) 2的结果为x2+□x+4,则“□”中的数为
A.-2 B.2 C.-4 D.4
相关试题

