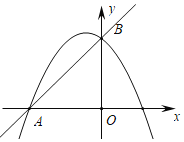
【题目】在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 经过点
经过点![]() 、
、![]() .
.
(1)求![]() 、
、![]() 满足的关系式及
满足的关系式及![]() 的值.
的值.
(2)当![]() 时,若
时,若![]() 的函数值随
的函数值随![]() 的增大而增大,求
的增大而增大,求![]() 的取值范围.
的取值范围.
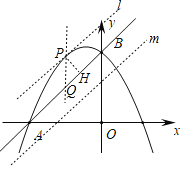
(3)如图,当![]() 时,在抛物线上是否存在点
时,在抛物线上是否存在点![]() ,使
,使![]() 的面积为1?若存在,请求出符合条件的所有点
的面积为1?若存在,请求出符合条件的所有点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)![]() ;
;![]() ;(2)
;(2)![]() ;(3)存在,点
;(3)存在,点![]() 或
或![]() 或
或![]() .
.
【解析】
(1)求出点![]() 、
、![]() 的坐标,即可求解;
的坐标,即可求解;
(2)当![]() 时,若
时,若![]() 的函数值随
的函数值随![]() 的增大而增大,则函数对称轴
的增大而增大,则函数对称轴![]() ,而
,而![]() ,即:
,即:![]() ,即可求解;
,即可求解;
(3)过点![]() 作直线
作直线![]() ,作
,作![]() 轴交
轴交![]() 于点
于点![]() ,作
,作![]() 于点
于点![]() ,
,![]() ,则
,则![]() ,即可求解.
,即可求解.
(1)![]() ,令
,令![]() ,则
,则![]() ,令
,令![]() ,则
,则![]() ,
,
故点![]() 、
、![]() 的坐标分别为
的坐标分别为![]() 、
、![]() ,则
,则![]() ,
,
则函数表达式为:![]() ,
,
将点![]() 坐标代入上式并整理得:
坐标代入上式并整理得:![]() ;
;
(2)当![]() 时,若
时,若![]() 的函数值随
的函数值随![]() 的增大而增大,
的增大而增大,
则函数对称轴![]() ,而
,而![]() ,
,
即:![]() ,解得:
,解得:![]() ,
,
故:![]() 的取值范围为:
的取值范围为:![]() ;
;
(3)当![]() 时,二次函数表达式为:
时,二次函数表达式为:![]() ,
,
过点![]() 作直线
作直线![]() ,作
,作![]() 轴交
轴交![]() 于点
于点![]() ,作
,作![]() 于点
于点![]() ,
,
∵![]() ,∴
,∴![]() ,
,
![]() ,
,
则![]() ,
,
在直线![]() 下方作直线
下方作直线![]() ,使直线
,使直线![]() 和
和![]() 与直线
与直线![]() 等距离,
等距离,
则直线![]() 与抛物线两个交点坐标,分别与点
与抛物线两个交点坐标,分别与点![]() 组成的三角形的面积也为1,
组成的三角形的面积也为1,
故:![]() ,
,
设点![]() ,则点
,则点![]() ,
,
即:![]() ,
,
解得:![]() 或
或![]() ,
,
故点![]() 或
或 ![]() 或
或![]() .
.
-
科目: 来源: 题型:
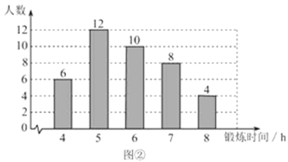
查看答案和解析>>【题目】为了解某校1000名学生一周在校参加体育锻炼的时间,现从各年级随机抽取了部分学生,对他们一周在校参加体育锻炼的时间进行了调查,并绘制出如下的统计图①和图②,根据相关信息,解答下列问题:
(Ⅰ)本次接受随机抽样调查的学生人数为 ,图①中
 的值为 ;
的值为 ;(Ⅱ)求本次调查获取的样本数据的平均数、众数和中位数;
(Ⅲ)根据样本数据,估计该校一周在校参加体育锻炼的时间大于
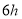 的学生人数.
的学生人数.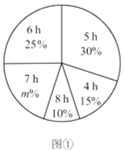
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在⊙O中,点C为
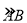 的中点,∠ACB=120°,OC的延长线与AD交于点D,且∠D=∠B.
的中点,∠ACB=120°,OC的延长线与AD交于点D,且∠D=∠B.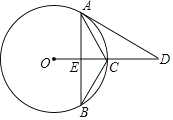
(1)求证:AD与⊙O相切;
(2)若CE=4,求弦AB的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某单位要将一份宣传资料进行批量印刷.在甲印刷厂,在收取100元制版费的基础上,每份收费0.5元;在乙印刷厂,在收取40元侧版费的基础上,每份收费0.7元.设该单位要印刷此宣传资料
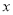 份(
份(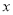 为正整数).
为正整数).(Ⅰ)根据题意,填写下表:
印剧数量(份)
150
250
350
450
…
甲印刷厂收费(元)
175
①
275
②
…
乙印刷厂收费(元)
145
215
③
355
…
(Ⅱ)设在甲印刷厂收费
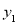 元,在乙印刷厂收费
元,在乙印刷厂收费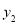 元,分别写出
元,分别写出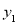 ,
,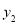 关于
关于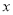 的函数解析式;
的函数解析式;(Ⅲ)当
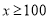 时,在哪家印刷厂花费少?请说明理由.
时,在哪家印刷厂花费少?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在⊙O中,AB是⊙O的直径,AB=10,
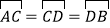 ,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:①∠BOE=60°;②∠CED=
,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:①∠BOE=60°;②∠CED= ∠DOB;③DM⊥CE;④CM+DM的最小值是10,上述结论中正确的个数是( )
∠DOB;③DM⊥CE;④CM+DM的最小值是10,上述结论中正确的个数是( )
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
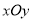 中,函数
中,函数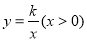 的图象与直线
的图象与直线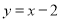 交于点A(3,m).
交于点A(3,m).(1)求k、m的值;
(2)已知点P(n,n)(n>0),过点P作平行于
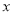 轴的直线,交直线y=x-2于点M,过点P作平行于y轴的直线,交函数
轴的直线,交直线y=x-2于点M,过点P作平行于y轴的直线,交函数 的图象于点N.
的图象于点N.①当n=1时,判断线段PM与PN的数量关系,并说明理由;
②若PN≥PM,结合函数的图象,直接写出n的取值范围.
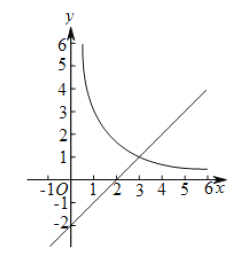
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的对角线AC,BD相交于点O,点E,F在BD上,BE=DF.
(1)求证:AE=CF;
(2)若AB=6,∠COD=60°,求矩形ABCD的面积.

相关试题

