【题目】如图,在四边形ABCD中,![]() ,
,![]() ,
,![]() ,
,![]() ,E是BC的中点,P是AB上的任意一点,连接PE,将PE绕点P逆时针旋转
,E是BC的中点,P是AB上的任意一点,连接PE,将PE绕点P逆时针旋转![]() 得到PQ,过A点,D点分别作BC的垂线,垂足分别为M,N.
得到PQ,过A点,D点分别作BC的垂线,垂足分别为M,N.

![]() 求AM的值;
求AM的值;
![]() 连接AC,若P是AB的中点,求PE的长;
连接AC,若P是AB的中点,求PE的长;
![]() 若点Q落在AB或AD边所在直线上,请直接写出BP的长.
若点Q落在AB或AD边所在直线上,请直接写出BP的长.
参考答案:
【答案】(1)12;(2)10;(3)PB的值为![]() 或
或![]() .
.
【解析】
![]() 作等腰梯形的双高,把问题转化为矩形,全等三角形即可解决问题;
作等腰梯形的双高,把问题转化为矩形,全等三角形即可解决问题;
![]() 如图2中,连接
如图2中,连接![]() 利用勾股定理求出AC,再利用三角形的中位线定理求出PE;
利用勾股定理求出AC,再利用三角形的中位线定理求出PE;
![]() 分两种情形分别讨论求解即可解决问题.
分两种情形分别讨论求解即可解决问题.
![]() 如图1中,作
如图1中,作![]() 用M,
用M,![]() 于N.
于N.

![]() ,
,
![]() ,
,
![]() ,
,
![]() 四边形AMND是矩形,
四边形AMND是矩形,
![]() ,
,
![]() ,
,
![]() ≌
≌![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() 如图2中,连接AC.
如图2中,连接AC.

在![]() 中,
中,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() 如图3中,当点Q落在直线AB上时,
如图3中,当点Q落在直线AB上时,

![]() ∽
∽![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
如图4中,当点Q在DA的延长线上时,作![]() 交DA的延长线于H,延长HP交BC于G.
交DA的延长线于H,延长HP交BC于G.

设![]() ,则
,则![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ≌
≌![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
综上所述,满足条件的PB的值为![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知关于x的方程kx=11﹣2x有整数解,则负整数k的值为 .
(2)若a+b+c=0,且a>b>c,以下结论:
①a>0,c>0;
②关于x的方程ax+b+c=0的解为x=1;
③a2=(b+c)2;
④
 的值为0或2;
的值为0或2;⑤在数轴上点A、B、C表示数a、b、c,若b<0,则线段AB与线段BC的大小关系是AB>BC.
其中正确的结论是 (填写正确结论的序号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AE是半圆O的直径,弦AB=BC=2
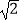 ,弦CD=DE=2,连结OB,OD,求图中两个阴影部分的面积和.
,弦CD=DE=2,连结OB,OD,求图中两个阴影部分的面积和. 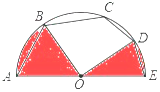
-
科目: 来源: 题型:
查看答案和解析>>【题目】某楼盘要对外销售
 该楼盘共23层,销售价格如下:第八层楼房售价为4000元
该楼盘共23层,销售价格如下:第八层楼房售价为4000元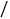 米
米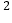 ,从第八层起每上升一层,每平方米的售价提高50元;反之,楼层每下降一层,每平方米的售价降低30元,
,从第八层起每上升一层,每平方米的售价提高50元;反之,楼层每下降一层,每平方米的售价降低30元,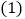 请写出售价
请写出售价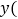 元
元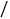 米
米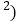 与楼层
与楼层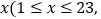 x取整数
x取整数 之间的函数关系式.
之间的函数关系式.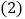 已知该楼盘每套楼房面积均为100米
已知该楼盘每套楼房面积均为100米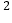 ,若购买者一次性付清所有房款,开发商有两种优惠方案:
,若购买者一次性付清所有房款,开发商有两种优惠方案:方案一:降价
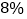 ,另外每套楼房总价再减a元;
,另外每套楼房总价再减a元;方案二:降价
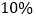 .
.老王要购买第十六层的一套楼房,若他一次性付清购房款,请帮他计算哪种优惠方案更加合算.
-
科目: 来源: 题型:
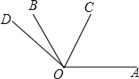
查看答案和解析>>【题目】如图,∠AOB=120°,射线OC从OA开始,绕点O逆时针旋转,旋转的速度为每分钟20°;射线OD从OB开始,绕点O逆时针旋转,旋转的速度为每分钟5°,OC和OD同时旋转,设旋转的时间为t(0≤t≤15).
(1)当t为何值时,射线OC与OD重合;
(2)当t为何值时,∠COD=90°;
(3)试探索:在射线OC与OD旋转的过程中,是否存在某个时刻,使得射线OC,OB与OD中的某一条射线是另两条射线所夹角的角平分线?若存在,请求出所有满足题意的t的取值,若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在ABCD中,E、F分别在BC、AD上,若想要使四边形AFCE为平行四边形,需添加一个条件,这个条件不可以是( )
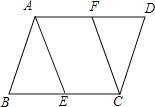
A. AF=CE B. AE=CF C. ∠BAE=∠FCD D. ∠BEA=∠FCE
-
科目: 来源: 题型:
查看答案和解析>>【题目】“城市发展,交通先行”,我市启动了缓堵保畅的高架桥快速通道建设工程,建成后将大大提升道路的通行能力.研究表明,某种情况下,高架桥上的车流速度V(单位:千米/时)是车流密度x(单位:辆/千米)的函数,且当0<x≤28时,V=80;当28<x≤188时,V是x的一次函数.函数关系如图所示.

(1)求当28<x≤188时,V关于x的函数表达式;
(2)请你直接写出车流量P和车流密度x之间的函数表达式;当x为多少时,车流量P(单位:辆/时)达到最大,最大值是多少?
(注:车流量是单位时间内通过观测点的车辆数,计算公式为:车流量=车流速度×车流密度)
相关试题

