【题目】探究
(1)已知如图1,若AB∥CD,P为平行线内的一点请你判断∠B+∠P+∠D= 度,并说明理由.
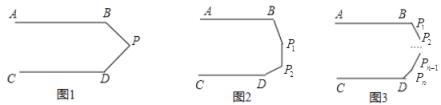
(2)如图2,若AB∥CD ,P1、P2为平行线内的两个点,请求出∠B+∠P1+∠P2+∠D= 度(不需要说明理由)
(3)如图3,如此类推若AB∥CD,P1、、P2、P3、P4、……Pn为平行线内的n个点,请求出∠B+∠P1+∠P2+∠P3+…….+∠Pn-1+∠Pn+∠D= 度(不需要说明理由)
参考答案:
【答案】(1)360°;(2)540°;(3)![]()
【解析】
(1)过点P作AB的平行线PE,利用平行线的性质,即可得到∠B+∠BPD+∠D=180°×2=360°;
(2)过P1作P1F∥AB,过P2作P2G∥CD,则利用平行线的性质,即可得到∠B+∠BP1P2+∠P1P2D+∠D的度数;
(3)利用(1)(2)中的结论,找出规律,即可得到∠A+∠C1+∠C2+……+∠Cn+1+∠D的度数.
解:(1)如图,过点P作AB的平行线PE,
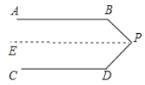
∵AB∥CD,AB∥PE,
∴∠B+∠BPE=180°,∠D+∠DPE=180°,
∵∠BPD=∠BPE+∠DPE,
∴∠B+∠BPD+∠D=180°×2=360°;
故答案为:360°.
(2)如图,过P1作C1F∥AB,过P2作P2G∥DE,
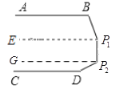
∵AB∥CD,P1F∥AB,过P2作P2G∥CD,
∴∠B+∠BP1F=180°,∠FP1P2+∠P1P2G=180°,∠GP2D+∠D=180°,
∵∠BP1P2=∠BP1F+∠FP1P2,∠P1P2D=∠P1P2G+∠GP2D,
∴∠B+∠BP1P2+∠P1P2D+∠D=180°×3=540°;
故答案为:540°.
(3)由(1)(2)可知,
当B、D两点之间有1个点时,∠B+∠BPD+∠D=180°×2=360°;
当B、D两点之间有2个点时,∠B+∠BP1P2+∠P1P2D+∠D=180°×3=540°;
……
当B、D两点之间有n个点时,有
∠A+∠C1+∠C2+……+∠Cn+1+∠D=180°(n+1);
故答案为:![]() .
.
-
科目: 来源: 题型:
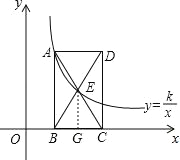
查看答案和解析>>【题目】已知如图:点(1,3)在函数y=
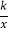 (x>0)的图象上,矩形ABCD的边BC在x轴上,E是对角线BD的中点,函数y=
(x>0)的图象上,矩形ABCD的边BC在x轴上,E是对角线BD的中点,函数y=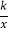 (x>0)的图象又经过A、E两点,点E的横坐标为m,解答下列问题:
(x>0)的图象又经过A、E两点,点E的横坐标为m,解答下列问题:(1)求k的值;
(2)求点A的坐标;(用含m代数式表示)
(3)当∠ABD=45°时,求m的值.
-
科目: 来源: 题型:
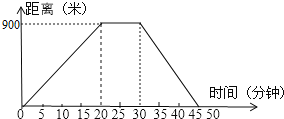
查看答案和解析>>【题目】如图,反映了小明从家里到超市的时间与距离之间关系的一幅图。
(1)图中自变量和因变量各是什么?
(2)小明到达超市用了多少时间?超市离家多远?
(3)分别求小明从家里到超市时的平均速度是多少?返回时的平均速度是多少?
-
科目: 来源: 题型:
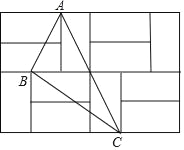
查看答案和解析>>【题目】如图,由12个形状、大小完全相同的小矩形组成一个大的矩形网格,小矩形的顶点称为这个矩形网格的格点,已知这个大矩形网格的宽为6,△ABC的顶点都在格点.
(1)求每个小矩形的长与宽;
(2)在矩形网格中找一格点E,使△ABE为直角三角形,求出所有满足条件的线段AE的长度.
(3)求sin∠BAC的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,∠BAC=60°,AB=AC,点D为直线BC上一动点(点D不与B,C重合),以AD为边在AD右侧作菱形ADEF,使∠DAF=60°,连接CF.
(1)观察猜想:如图1,当点D在线段BC上时,①AB与CF的位置关系为: ;
②BC,CD,CF之间的数量关系为: .
(2)数学思考:如图2,当点D在线段CB的延长线上时,结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.
(3)拓展延伸:如图3,当点D在线段BC的延长线上时,设AD与CF相交于点G,若已知AB=4,CD=
 AB,求AG的长.
AB,求AG的长.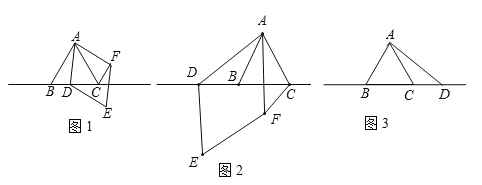
-
科目: 来源: 题型:
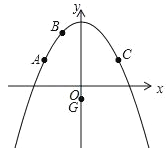
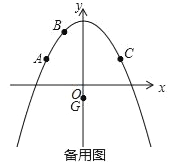
查看答案和解析>>【题目】二次函数y=ax2+c的图象经过点A(﹣4,3),B(﹣2,6),点A关于抛物线对称轴的对称点为点C,点P是抛物线对称轴右侧图象上的一点,点G(0,﹣1).
(1)求出点C坐标及抛物线的解析式;
(2)若以A,C,P,G为顶点的四边形面积等于30时,求点P的坐标;
(3)若Q为线段AC上一动点,过点Q平行于y轴的直线与过点G平行于x轴的直线交于点M,将△QGM沿QG翻折得到△QGN,当点N在坐标轴上时,求Q点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
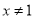 ,计算
,计算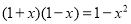 ,
,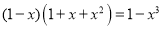 ,
,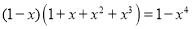 .
.猜想:
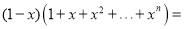 (n为正整数);
(n为正整数);(1)根据你的猜想计算:
①
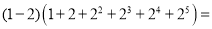
②
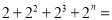 (n为正整数)
(n为正整数)③
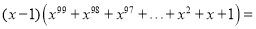
(2)通过以上规律请你进行下面的探索:
①
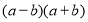
②
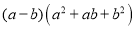
③
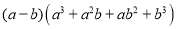
(3)判断
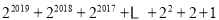 的个位数字是
的个位数字是
相关试题

