Question

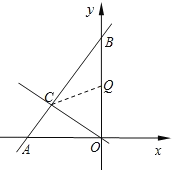
【题目】如图，一次函数的图像与的图像交于点，与轴和 轴分别交于点和点，且点的横坐标为.

(1)求的值与的长;

(2)若点为线段上一点，且，求点的坐标.

Answer 1

【答案】(1) ，；(2) .

【解析】

（1）把点C的横坐标代入正比例函数解析式，求得点C的纵坐标，然后把点C的坐标代入一次函数解析式即可求得m的值，从而得到一次函数的解析式，则易求点A、B的坐标，然后根据勾股定理即可求得AB；
（2）由得到OQ的长，即可求得Q点的坐标．

(1)∵点C在直线上，点C的横坐标为3，

∴点C坐标为

又∵点C在直线y=mx+2m+3上，

∴

∴

∴直线AB的函数表达式为

令x=0,则y=6,令y=0,则，解得x=4，

∴A(4,0)、B(0,6)，

∴

(2)∵，

∴

∴OQ=2，

∴点Q坐标为(0,2).