【题目】感知:如图1,AD平分∠BAC.∠B+∠C=180°,∠B=90°,易知:DB=DC.
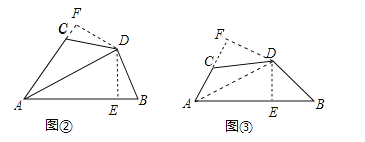
探究:如图2,AD平分∠BAC,∠ABD+∠ACD=180°,∠ABD<90°,求证:DB=DC.
应用:如图3,四边形ABCD中,∠B=45°,∠C=135°,DB=DC=a,则AB﹣AC= (用含a的代数式表示)

参考答案:
【答案】探究:证明见解析;应用:![]() a.
a.
【解析】
试题分析:探究:欲证明DB=DC,只要证明△DFC≌△DEB即可.
应用:先证明△DFC≌△DEB,再证明△ADF≌△ADE,结合BD=![]() EB即可解决问题.
EB即可解决问题.
试题解析:探究:
证明:如图②中,DE⊥AB于E,DF⊥AC于F,∵DA平分∠BAC,DE⊥AB,DF⊥AC,∴DE=DF,∵∠B+∠ACD=180°,∠ACD+∠FCD=180°,∴∠B=∠FCD,在△DFC和△DEB中,∵∠F=∠DEB,∠FCD=∠B,DF=DB,∴△DFC≌△DEB,∴DC=DB.
应用:解;如图③连接AD、DE⊥AB于E,DF⊥AC于F,∵∠B+∠ACD=180°,∠ACD+∠FCD=180°,∴∠B=∠FCD,在△DFC和△DEB中,∵∠F=∠DEB,∠FCD=∠B,DC=DB,∴△DFC≌△DEB,∴DF=DE,CF=BE,在RT△ADF和RT△ADE中,∵AD=AD,DE=DF,∴△ADF≌△ADE,∴AF=AE,∴AB﹣AC=(AE+BE)﹣(AF﹣CF)=2BE,在RT△DEB中,∵∠DEB=90°,∠B=∠EDB=45°,BD=a,∴BE=![]() a,∴AB﹣AC=
a,∴AB﹣AC=![]() a.故答案为:
a.故答案为:![]() a.
a.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,一块等腰直角三角形铁板,通过切割焊接成一个含有45°角的平行四边形,设计一种简要的方案并给出正确的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,D是BC边的中点,E、F分别在AD及其延长线上,CE∥BF,连结BE、CF.
(1)图中的四边形BFCE是平行四边形吗?为什么?
(2)若AB=AC,其它条件不变,那么四边形BFCE是菱形吗?为什么? -
科目: 来源: 题型:
查看答案和解析>>【题目】要反映一天内气温的变化情况宜采用( )
A. 条形统计图 B. 扇形统计图 C. 折线统计图 D. 频数分布图
-
科目: 来源: 题型:
查看答案和解析>>【题目】两个有理数a、b在数轴上的位置如图所示,则a+b0;ab0(填“<”或“>”).
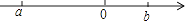
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,分别延长ABCD的边CD,AB到E,F,使DE=BF,连接EF,分别交AD,BC于G,H,连结CG,AH.
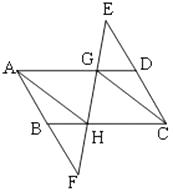
求证:CG∥AH. -
科目: 来源: 题型:
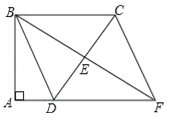
查看答案和解析>>【题目】如图,四边形ABCD中,∠A=∠ABC=90°,AD=10cm,BC=30cm,E是边CD的中点,连接BE并延长与AD的延长线相交于点F.
(1)求证:四边形BDFC是平行四边形;
(2)若△BCD是等腰三角形,求四边形BDFC的面积.
相关试题

