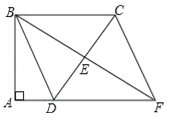
【题目】如图,四边形ABCD中,∠A=∠ABC=90°,AD=10cm,BC=30cm,E是边CD的中点,连接BE并延长与AD的延长线相交于点F.
(1)求证:四边形BDFC是平行四边形;
(2)若△BCD是等腰三角形,求四边形BDFC的面积.
参考答案:
【答案】(1)证明见解析;(2)![]() cm2或
cm2或![]() cm2.
cm2.
【解析】
试题分析:(1)根据同旁内角互补两直线平行求出BC∥AD,再根据两直线平行,内错角相等可得∠CBE=∠DFE,然后利用“角角边”证明△BEC和△FCD全等,根据全等三角形对应边相等可得BE=EF,然后利用对角线互相平分的四边形是平行四边形证明即可;
(2)分三种情况:①BC=BD时,由勾股定理列式求出AB,由平行四边形的面积公式列式计算即可得解;
②BC=CD时,过点C作CG⊥AF于G,证出四边形AGCB是矩形,由矩形的对边相等得AG=BC=3,求出DG=2,由勾股定理列式求出CG,由平行四边形的面积列式计算即可;
③BD=CD时,BC边上的中线应该与BC垂直,从而得到BC=2AD=2,矛盾.
试题解析:(1)证明:∵∠A=∠ABC=90°,∴BC∥AD,∴∠CBE=∠DFE,在△BEC与△FED中,∵∠CBE=∠DFE,∠BEC=∠FED,CE=DE,∴△BEC≌△FED(AAS),∴BE=FE,又∵E是边CD的中点,∴CE=DE,∴四边形BDFC是平行四边形;
(2)解:分三种情况:①BC=BD=30cm时,由勾股定理得,AB=![]() =
=![]() =
=![]() (cm),∴四边形BDFC的面积=
(cm),∴四边形BDFC的面积=![]() =
=![]() (cm2);
(cm2);
②BC=CD=30时,过点C作CG⊥AF于G,如图所示:
则四边形AGCB是矩形,∴AG=BC=30,∴DG=AG﹣AD=30﹣10=20,由勾股定理得,CG=![]() =
=![]() =
=![]() ,∴四边形BDFC的面积=
,∴四边形BDFC的面积=![]() =
=![]() ;
;
③BD=CD时,BC边上的中线应该与BC垂直,从而得到BC=2AD=20,矛盾,此时不成立;
综上所述,四边形BDFC的面积是![]() cm2或
cm2或![]() cm2.
cm2.
-
科目: 来源: 题型:
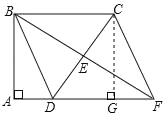
查看答案和解析>>【题目】感知:如图1,AD平分∠BAC.∠B+∠C=180°,∠B=90°,易知:DB=DC.
探究:如图2,AD平分∠BAC,∠ABD+∠ACD=180°,∠ABD<90°,求证:DB=DC.
应用:如图3,四边形ABCD中,∠B=45°,∠C=135°,DB=DC=a,则AB﹣AC= (用含a的代数式表示)

-
科目: 来源: 题型:
查看答案和解析>>【题目】两个有理数a、b在数轴上的位置如图所示,则a+b0;ab0(填“<”或“>”).
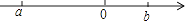
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,分别延长ABCD的边CD,AB到E,F,使DE=BF,连接EF,分别交AD,BC于G,H,连结CG,AH.
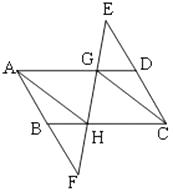
求证:CG∥AH. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD为平行四边形,∠BAD的角平分线AF交CD于点E,交BC的延长线于点F.
(1)求证:BF=CD;
(2)连接BE,若BE⊥AF,∠BFA=60°,BE=
 ,求平行四边形ABCD的周长.
,求平行四边形ABCD的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程
(1)2x2+5x=3;
(2)(x﹣7)(x+3)=2x﹣14.
相关试题

