【题目】如图所示,一块等腰直角三角形铁板,通过切割焊接成一个含有45°角的平行四边形,设计一种简要的方案并给出正确的理由. 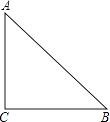
参考答案:
【答案】解:如图,取AC、BC的中点E、D,连接ED,沿ED切割,固定点E,△ECD旋转180°使C点与A点重合即可. 
理由:在Rt△ABC中,
∵AC=BC,∠B=45°,
又∵E、D分别是AC、BC的中点,
∴EC=DC
∴∠CED=∠CDE=45°
∴∠AEF=∠CED=45°
∴∠AEF+∠AED=∠CED+∠AED=180°
∴F、E、D在一条直线上.
又∵∠EAF=∠C=90°
∴AF∥CD.
又∵AF=CD=DB,
∴四边形AFDB是平行四边形,且∠B=45°
【解析】∵这是一块等腰直角三角形铁板,已经包含45°的角.∴应用到题中45°的角,利用全等进行割补,应遵循简单易行的原则.
【考点精析】掌握等腰直角三角形和平行四边形的判定与性质是解答本题的根本,需要知道等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】能够找到一点,使该点到各边的距离相等的为( )①平行四边形;②菱形;③矩形;④正方形.
A.①与②B.②与③C.②与④D.③与④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,E,F分别是AB,CD的中点,G,H分别是AF,CE的中点,连结EG,FH.
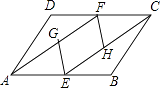
(1)四边形EHFG是不是平行四边形?如果是,请给出证明;如果不是,请说明理由;
(2)求四边形EHFG的面积与平行四边形ABCD的面积之比. -
科目: 来源: 题型:
查看答案和解析>>【题目】作图题(保留作图痕迹,不写画法).
(1)请在坐标系中,画出△ABC关于y轴对称的△A′B′C′.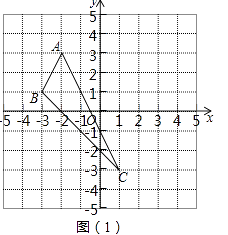
(2)如图(2),A与B是两个居住社区,OC与OD是两条交汇的公路,欲建立一个超市M,使它到A、B两个社区的距离相等,且到两条公路OC、OD的距离也相等.请利用尺规作图,确定超市M的位置.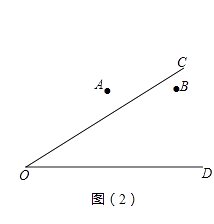
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,D是BC边的中点,E、F分别在AD及其延长线上,CE∥BF,连结BE、CF.
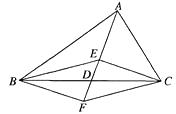
(1)图中的四边形BFCE是平行四边形吗?为什么?
(2)若AB=AC,其它条件不变,那么四边形BFCE是菱形吗?为什么? -
科目: 来源: 题型:
查看答案和解析>>【题目】要反映一天内气温的变化情况宜采用( )
A. 条形统计图 B. 扇形统计图 C. 折线统计图 D. 频数分布图
-
科目: 来源: 题型:
查看答案和解析>>【题目】感知:如图1,AD平分∠BAC.∠B+∠C=180°,∠B=90°,易知:DB=DC.
探究:如图2,AD平分∠BAC,∠ABD+∠ACD=180°,∠ABD<90°,求证:DB=DC.
应用:如图3,四边形ABCD中,∠B=45°,∠C=135°,DB=DC=a,则AB﹣AC= (用含a的代数式表示)

相关试题

