【题目】三角形的两边长分别为3和5,要使这个三角形是直角三角形,则第三边长是 .
参考答案:
【答案】4或 ![]()
【解析】解:当第三边是直角边时,根据勾股定理,第三边的长= ![]() =4,三角形的边长分别为3,4,5能构成三角形;
=4,三角形的边长分别为3,4,5能构成三角形;
当第三边是斜边时,根据勾股定理,第三边的长= ![]() =
= ![]() ,三角形的边长分别为3,5,
,三角形的边长分别为3,5, ![]() 亦能构成三角形;
亦能构成三角形;
综合以上两种情况,第三边的长应为4或 ![]() .
.
【考点精析】根据题目的已知条件,利用三角形三边关系和勾股定理的逆定理的相关知识可以得到问题的答案,需要掌握三角形两边之和大于第三边;三角形两边之差小于第三边;不符合定理的三条线段,不能组成三角形的三边;如果三角形的三边长a、b、c有下面关系:a2+b2=c2,那么这个三角形是直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AQ=PQ,PR=PS,PR⊥AB于R,PS⊥AC于S,则三个结论:①AS=AR,②QP∥AR,③△BPR≌△QPS中一定正确的是( )
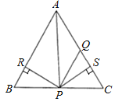
A. 全部正确 B. 仅①和②正确 C. 仅①正确 D. 仅①和③正确
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,AB=1,连接AC,以AC为边作第一个正方形ACC1D1 , 连接AC1 , 以AC1为边作第二个正方形AC1C2D2 , 则第10个正方形边长为( )
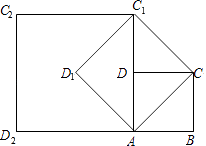
A.8
B.16
C.32
D.64 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD.图中的CE、BD有怎样的大小和位置关系?试证明你的结论.
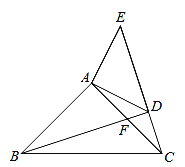
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,M在DC上,且BM=10,N是AC上一动点,则DN+MN的最小值为 .
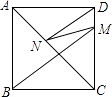
-
科目: 来源: 题型:
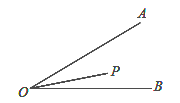
查看答案和解析>>【题目】如图,已知∠AOB=30°,P为其内部一点,OP=3,M、N分别为OA、OB边上的一点,要使△PMN的周长最小,请给出确定点M、N位置的方法,并求出最小周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,∠A=30°,∠B=60°。
(1)作∠B的平分线BD,交AC于点D;作AB的中点E(要求:尺规作图,保留作图痕迹)
(2)连接DE,求证:△ADE≌△BDE。

相关试题

