【题目】如图,过点A(2,0)的两条直线l1,l2分别交y轴于点B,C,其中点B在原点上方,点C在原点下方,已知AB=![]() .
.
(1)求点B的坐标;
(2)若△ABC的面积为4,求直线l2的解析式.

参考答案:
【答案】(1)点B的坐标为(0,3);(2)l2的解析式为y=![]() x-1.
x-1.
【解析】(1)先根据勾股定理求得BO的长,再写出点B的坐标;(2)先根据△ABC的面积4,求得CO的长,再根据点A、C的坐标运用待定系数法求得直线l2的解析式.
解:(1)∵点A(2,0),AB=![]()
∴BO=![]() =3
=3
∴点B的坐标为(0,3);
(2)∵△ABC的面积为4 ∴![]() ×BC×AO=4 ∴
×BC×AO=4 ∴![]() ×BC×2=4,即BC=4
×BC×2=4,即BC=4
∵BO=3 ∴CO=4﹣3=1 ∴C(0,﹣1)
设l2的解析式为y=kx+b,则![]() ,解得
,解得 ,
,
∴l2的解析式为y=![]() x﹣1.
x﹣1.
“点睛”本题主要考查了两条直线的交点问题,解题的关键是掌握勾股定理以及待定系数法.注意:两条直线的交点坐标,就是由这两条直线相对应的一次函数的表达式所组成二元一次过程组的解,反之也成立.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题是真命题的是( )
A.内错角相等
B.平面内,过一点有且只有一条直线与已知直线垂直
C.相等的角是对顶角
D.过一点有且只有一条直线与已知直线平行
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P是等边△ABC内一点,PA=6,PB=8,PC=10,则△APC的面积是__________

-
科目: 来源: 题型:
查看答案和解析>>【题目】射阳县实验初中为了解全校学生上学期参加社区活动的情况,学校随机调查了本校50名学生参加社区活动的次数,并将调查所得的数据整理如下:
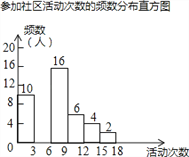
参加社区活动次数的频数、频率分布表
活动次数x
频数
频率
0<x≤3
10
0.20
3<x≤6
a
0.24
6<x≤9
16
0.32
9<x≤12
6
0.12
12<x≤15
m
b
15<x≤18
2
n
根据以上图表信息,解答下列问题:
(1)表中a= ,b= ;
(2)请把频数分布直方图补充完整(画图后请标注相应的数据);
(3)若该校共有1200名学生,请估计该校在上学期参加社区活动超过6次的学生有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于平面直角坐标系xOy中的点P(a,b),若点P′的坐标为(a+kb,ka+b)(其中k为常数,且k≠0),则称点P′为点P的“k属派生点”.
例如:P(1,4)的“2属派生点”为P′(1+2×4,2×1+4),即P′(9,6).
(1)点P(-1,6)的“2属派生点”P′的坐标为_____________;
(2)若点P的“3属派生点”P′的坐标为(6,2),则点P的坐标___________;
(3)若点P在x轴的正半轴上,点P的“k属派生点”为P′点,且线段PP′的长度为线段OP长度的2倍,求k的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,分别以点A和点B为圆心,大于
 AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若△ADC的周长为10,AB=7,则△ABC的周长为 .
AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若△ADC的周长为10,AB=7,则△ABC的周长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在ABCD中,E,F分别是边AD,BC上的点,且AE=CF,直线EF分别交BA的延长线、DC的延长线于点G,H,交BD于点O.
(1)求证:△ABE≌△CDF;
(2)连接DG,若DG=BG,则四边形BEDF是什么特殊四边形?请说明理由.

相关试题

