【题目】如图,正方形ABCD的边长为8,在各边上顺次截取AE=BF=CG=DH=5,则四边形EFGH的面积是______.

参考答案:
【答案】34
【解析】
由正方形的性质得出∠A=∠B=∠C=∠D=90°,AB=BC=CD=DA,证出AH=BE=CF=DG,由SAS证明△AEH≌△BFE≌△CGF≌△DHG,得出EH=FE=GF=GH,∠AEH=∠BFE,证出四边形EFGH是菱形,再证出∠HEF=90°,即可得出四边形EFGH是正方形,由勾股定理得EH,即可得出正方形EFGH的面积.
∵四边形ABCD是正方形,
∴∠A=∠B=∠C=∠D=90°,AB=BC=CD=DA,
∵AE=BF=CG=DH,
∴AH=BE=CF=DG.
在△AEH、△BFE、△CGF和△DHG中,

∴△AEH≌△BFE≌△CGF≌△DHG(SAS),
∴EH=FE=GF=GH,∠AEH=∠BFE,
∴四边形EFGH是菱形,
∵∠BEF+∠BFE=90°,
∴∠BEF+∠AEH=90°,
∴∠HEF=90°,
∴四边形EFGH是正方形,
∵AB=BC=CD=DA=8,AE=BF=CG=DH=5,
∴EH=FE=GF=GH=![]()
所以正方形EFGH的面积![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A,B,C,D为矩形的四个顶点,AB=16 cm,AD=6 cm,动点P,Q分别从点A,C同时出发,点P以3 cm/s的速度向点B移动,一直到点B为止,点Q以2 cm/s的速度向点D移动,当点P停止运动时,点Q也停止运动.问:
(1)P,Q两点从开始出发多长时间时,四边形PBCQ的面积是33 cm2?
(2)P,Q两点从开始出发多长时间时,点P与点Q之间的距离是10 cm?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,PA、PB切⊙O于A、B两点,CD切⊙O于点E,交PA,PB于C、D,若⊙O的半径为r,△PCD的周长等于3r,则tan∠APB的值是( )
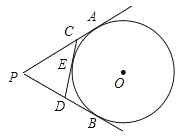
A.
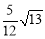 B.
B.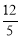 C.
C. D.
D.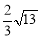
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一条直线过点
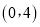 ,且与抛物线
,且与抛物线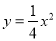 交于A、B两点,其中点A的横坐标是-2.
交于A、B两点,其中点A的横坐标是-2.⑴求这条直线的函数关系式及点B的坐标 ;
⑵在
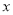 轴上是否存在点C,使得ABC是直角三角形?若存在,求出点C的坐标,若不存在,请说明理由;
轴上是否存在点C,使得ABC是直角三角形?若存在,求出点C的坐标,若不存在,请说明理由; ⑶.过线段AB上一点P,作PM∥
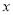 轴,交抛物线于点M,点M在第一象限;点
轴,交抛物线于点M,点M在第一象限;点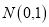 ,当点M的横坐标为何值时,MN+3MP的长度最大?最大值是多少?
,当点M的横坐标为何值时,MN+3MP的长度最大?最大值是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,
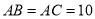 ,线段
,线段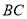 在轴上,
在轴上, 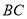 =12,点
=12,点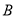 的坐标为(-3,0),线段
的坐标为(-3,0),线段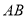 交
交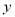 轴于点
轴于点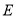 ,过
,过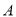 作
作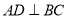 于
于 ,动点
,动点 从原点出发,以每秒3个单位的速度沿
从原点出发,以每秒3个单位的速度沿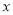 轴向右运动,设运动的时间为
轴向右运动,设运动的时间为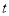 秒.
秒.(1)点
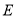 的坐标为(_________),__________);
的坐标为(_________),__________);(2)当
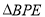 是等腰三角形时,求
是等腰三角形时,求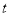 的值;
的值;(3)若点
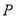 运动的同时,
运动的同时, 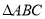 以
以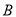 为位似中心向右放大,且点
为位似中心向右放大,且点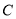 向右运动的速度为每秒2个单位,
向右运动的速度为每秒2个单位, 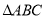 放大的同时高
放大的同时高 也随之放大,当以
也随之放大,当以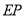 为直径的圆与动线段
为直径的圆与动线段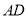 所在直线相切,求
所在直线相切,求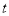 的值和此时C点的坐标.
的值和此时C点的坐标.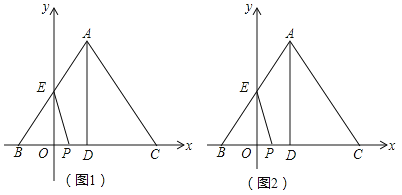
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
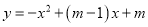 .
.(1)证明:不论
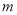 取何值,该函数图像与
取何值,该函数图像与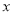 轴总有公共点;
轴总有公共点;(2)若该函数的图像与
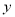 轴交于点(0,3),求出顶点坐标并画出该函数图像;
轴交于点(0,3),求出顶点坐标并画出该函数图像;(3)在(2)的条件下,观察图像,解答下列问题:
①不等式
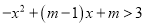 的的解集是 ;
的的解集是 ;②若一元二次方程
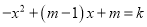 有两个不相等的实数根,则
有两个不相等的实数根,则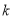 的取值范围是 ;
的取值范围是 ;③若一元二次方程
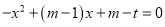 在
在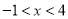 的范围内有实数根,则
的范围内有实数根,则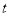 的取
的取值范围是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们规定:相等的实数看作同一个实数.有下列六种说法:
①数轴上有无数多个表示无理数的点;
②带根号的数不一定是无理数;
③每个有理数都可以用数轴上唯一的点来表示;
④数轴上每一个点都表示唯一一个实数;
⑤没有最大的负实数,但有最小的正实数;
⑥没有最大的正整数,但有最小的正整数.
其中说法错误的有_____(注:填写出所有错误说法的编号)
相关试题

