Question

【题目】如图（a），直线l1：y＝kx+b经过点A、B，OA＝OB＝3，直线12：y＝x﹣2交y轴于点C，且与直线l1交于点D，连接OD．

（1）求直线11的表达式；

（2）求△OCD的面积；

（3）如图（b），点P是直线11上的一动点；连接CP交线段OD于点E，当△COE与△DEP的面积相等时，求点P的坐标．

Answer 1

【答案】（1）y＝﹣x+3；（2）△OCD的面积＝2；（3）点P（，）．

【解析】

（1）OA＝OB＝3，则点A、B的坐标分别为：（3，0）、（0，3），将点A、B的坐标代入一次函数表达式，即可求解；

（2）联立l1、l2的表达式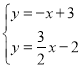得：，解得：，故点D（2，1），最后用三角形的面积公式即可得出结论；

（3）△COE与△DEP的面积相等，则S△CDO＝S△PCD，则点P、O到CD的距离相等，故OP所在的直线与CD平行，即可求解．

（1）OA＝OB＝3，则点A、B的坐标分别为：（3，0）、（0，3），

将点A、B的坐标代入一次函数表达式：y＝kx+b得：，解得：，

故直线11的表达式为：y＝﹣x+3…①；

（2）联立l1、l2的表达式得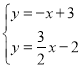：，解得：，故点D（2，1）；

令x=0, y＝x﹣2,

∴C（0，-2）

故OC=2

△OCD的面积＝×OCxD＝×2×2＝2；

（3）△COE与△DEP的面积相等，

则S△CDO＝S△CDE+S△OCE＝S△PED+S△CED＝S△PCD，

则点P、O到CD的距离相等，故OP所在的直线与CD平行，

则直线OP的表达式为：y＝x…②，

联立①②并解得：x＝，

则点P（，）．