【题目】余姚某特产专卖店销售核桃,其进价为每千克40元,按每千克60元销售,平均每天可售出100千克,后来经过市场调查发现,单价每降低1元,则平均每天的销量可增加10千克.(销售利润=销售价—进价)
(1)如果每千克核桃降价![]() 元,那么每千克核桃的销售利润为________元,平均每天可销售_________千克;(用含
元,那么每千克核桃的销售利润为________元,平均每天可销售_________千克;(用含![]() 的代数式表示)
的代数式表示)
(2)若该专卖店销售这种核桃想要平均每天获利2240元,每千克核桃应降价多少元?
(3)在(2)条件下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折销售?
参考答案:
【答案】(1)![]() ,
,![]() ;(2)应降价4元或6元;(3)九折.
;(2)应降价4元或6元;(3)九折.
【解析】
(1)依题意直接可用含x的代数式表示即可;
(2)根据每天的利润=每千克的利润×每天的销量,结合(1)可以列出关于x的方程求解即可;
(3)根据(2)中的答案,结合尽可能让利于顾客,赢得市场,确定降价6元,从而得到销售折扣.
解:(1)原来每千克的利润为60-40=20元,现在每千克降价x元,故每千克的销售利润为![]() 元,又根据单价每降低1元,则平均每天的销量可增加10千克,可知现在平均每天的销量为
元,又根据单价每降低1元,则平均每天的销量可增加10千克,可知现在平均每天的销量为![]() 千克;
千克;
故答案为:![]() ,
,![]()
(2)设每千克核桃应降价x元,
(60-x-40)(100+10x)=2240,
整理得:![]()
解得,x1=4,x2=6,
即每千克核桃应降价4元或6元;
(3)由(2)可知每千克核桃可降价4元或6元,
∵要尽可能让利于顾客,
∴每千克核桃应降价6元,此时售价为:60-6=54(元),
∴![]()
即该店应按原价的九折出售;
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)先化简,再求值:当(x﹣2)2+|y+1|=0时,求代数式4(
 x2﹣3xy﹣y2)﹣3(x2﹣7xy﹣2y2)的值;
x2﹣3xy﹣y2)﹣3(x2﹣7xy﹣2y2)的值;(2)关于x的代数式(x2+2x)﹣[kx2﹣(3x2﹣2x+1)]的值与x无关,求k的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在全民读书月活动中,某校随机抽样调查了一部分学生本学期计划购买课外书的费用情况,根据图中的相关信息,解答下面问题;
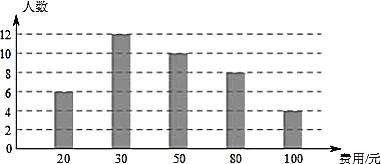
(1)这次调查获取的样本容量是________;
(2)由统计图可知,这次调查获取的样本数据的众数是________;中位数是________;
(3)若该校共有1000名学生,根据样本数据,估计该校本学期计划购买课外书的总花费.
-
科目: 来源: 题型:
查看答案和解析>>【题目】滴滴快车是一种便捷的出行工具,其计价规则如图:

(注:滴滴快车车费由里程费、时长费、远途费三部分构成,其中里程费按行车的具体时段标准和实际里程计算:时长费按具体时段标准和行车的实际时间计算,远途费的收取方式:行车里程10公里以内(含10公里)不收远途费,超过10公里的,超出部分每公里收0.3元)
(1)小红早上7:00从家出发乘坐滴滴快车到学校,行驶里程2公里,用时8分钟,需付车费 元,傍晚17:00放学乘坐滴滴快车到妈妈单位,行驶里程5公里,用时20分钟,需付车费 元;
(2)某人06:10出发,乘坐滴滴快车到某地,行驶里程20公里,用时40分钟,需付车费多少元?
(3)某人普通时段乘坐演滴快车到某地,用时30分钟,共花车费39.8元,求他行驶的里程?
-
科目: 来源: 题型:
查看答案和解析>>【题目】制作一种产品,需先将材料加热达到60 ℃后,再进行操作.设该材料温度为y(℃),从加热开始计算的时间为x(min).据了解,当该材料加热时,温度y与时间x成一次函数关系;停止加热进行操作时,温度y与时间x成反比例关系(如图).已知该材料在操作加热前的温度为15 ℃,加热5分钟后温度达到60 ℃.

(1)分别求出将材料加热和停止加热进行操作时,y与x的函数关系式;
(2)根据工艺要求,当材料的温度低于15 ℃时,须停止操作,那么从开始加热到停止操作,共经历了多少时间?
-
科目: 来源: 题型:
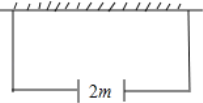
查看答案和解析>>【题目】如图,某农户准备建一个长方形养鸡场,养鸡场的一边靠墙,墙对面有一个2m宽的门,另三边用竹篱笆围成,篱笆总长33m.围成长方形的养鸡场除门之外四周不能有空隙.
(1)若墙长为18m,要围成养鸡场的面积为150m2,则养鸡场的长和宽各为多少?
(2)围成养鸡场的面积能否达到200m2?请说明理由
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:点A是双曲线
 在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为一边作等边三角形ABC,点C在第四象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式是( )
在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为一边作等边三角形ABC,点C在第四象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式是( )A.
 B.
B.  C.
C.  D.
D. 
相关试题

