Question

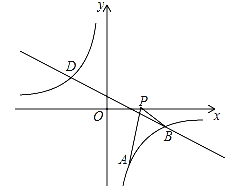
【题目】如图，已知点A（1，a）是反比例函数的图象上一点，直线与反比例函数的图象的交点为点B、D，且B（3，﹣1），求：

（1）求反比例函数的解析式；

（2）求点D坐标，并直接写出y1＞y2时x的取值范围；

（3）动点P（x，0）在x轴的正半轴上运动，当线段PA与线段PB之差达到最大时，求点P的坐标．

Answer 1

【答案】（1）；（2）D（－2，），－2＜x＜0，或x＞3；（3）P（4，0）．

【解析】试题分析：（1）把点B（3，﹣1）带入反比例函数中，即可求得k的值；

（2）联立直线和反比例函数的解析式构成方程组，化简为一个一元二次方程，解方程即可得到点D坐标，观察图象可得相应x的取值范围；

（3）把A（1，a）是反比例函数的解析式，求得a的值，可得点A坐标，用待定系数法求得直线AB的解析式，令y=0，解得x的值，即可求得点P的坐标.

试题解析：（1）∵B（3，﹣1）在反比例函数的图象上，

∴-1=，

∴m=-3，

∴反比例函数的解析式为；

（2），

∴=，

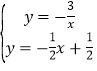x2-x-6=0，

（x-3）（x+2）=0，

x1=3，x2=-2，

当x=-2时，y=，

∴D（－2，）；

y1＞y2时x的取值范围是-2<x<0或x>；

（3）∵A（1，a）是反比例函数的图象上一点，

∴a=-3，

∴A（1，-3），

设直线AB为y=kx+b,

，

∴，

∴直线AB为y=x-4，

令y=0，则x=4，

∴P(4，0)