【题目】如图,点O是等边△ABC内一点,∠AOB=100°,∠BOC=α.以OC为一边作等边三角形OCD,连接AC、AD.

(1)当α=150°时,试判断△AOD的形状,并说明理由;
(2)当△AOD是等腰三角形时,求α的度数.
参考答案:
【答案】(1)△OCD是等边三角形,理由见解析;(2)当α为130°、100°、160°时,△AOD是等腰三角形.
【解析】
试题分析:(1)首先根据已知条件可以证明△BOC≌△ADC,然后利用全等三角形的性质可以求出∠ADO的度数,由此即可判定△AOD的形状;
(2)利用(1)和已知条件及等腰三角形的性质即可求解.
解:(1)∵△OCD是等边三角形,
∴OC=CD,
∵△ABC是等边三角形,
∴BC=AC,
∵∠ACB=∠OCD=60°,
∴∠BCO=∠ACD,
在△BOC与△ADC中,
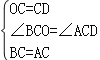 ,
,
∴△BOC≌△ADC,
∴∠BOC=∠ADC,
∵∠BOC=α=150°,∠ODC=60°,
∴∠ADO=150°﹣60°=90°,
∴△ADO是直角三角形;
(2)∵∠COB=∠CAD=α,∠AOD=200°﹣α,∠ADO=α﹣60°,∠OAD=40°,
①要使AO=AD,需∠AOD=∠ADO,
∴200°﹣α=α﹣60°,
∴α=130°;
②要使OA=OD,需∠OAD=∠ADO,
∴α﹣60°=40°,
∴α=100°;
③要使OD=AD,需∠OAD=∠AOD,
∴200°﹣α=40°,
∴α=160°.
所以当α为130°、100°、160°时,△AOD是等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】|a|=1,|b|=4,且ab<0,则a+b的值为( )
A. 3 B. ﹣3 C. ±3 D. ±5
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a和b互为倒数,则(ab)2002011=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两家草莓采摘园的草莓品质相同,销售价格也相同.“五一期间”,两家均推出了优惠方案,甲采摘园的优惠方案是:游客进园需购买50元的门票,采摘的草莓六折优惠;乙采摘园的优惠方案是:游客进园不需购买门票,采摘园的草莓超过一定数量后,超过部分打折优惠.优惠期间,设某游客的草莓采摘量为x(千克),在甲采摘园所需总费用为
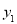 (元),在乙采摘园所需总费用为
(元),在乙采摘园所需总费用为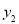 (元),图中折线OAB表示
(元),图中折线OAB表示 与x之间的函数关系.
与x之间的函数关系.(1)甲、乙两采摘园优惠前的草莓销售价格是每千克 元;
(2)求
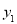 、
、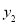 与x的函数表达式;
与x的函数表达式;(3)在图中画出
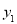 与x的函数图象,并写出选择甲采摘园所需总费用较少时,草莓采摘量x的范围.
与x的函数图象,并写出选择甲采摘园所需总费用较少时,草莓采摘量x的范围.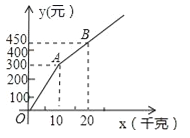
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题,其中是真命题的为( )
A.一组对边平行,另一组对边相等的四边形是平行四边形
B.一组邻边相等的矩形是正方形
C.对角线相等的四边形是矩形
D.对角线互相垂直的四边形是菱形
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.对角线互相垂直且相等的四边形是菱形B.对角线相等的四边形是矩形
C.对角线互相垂直的四边形是平行四边形D.对角线相等且互相平分的四边形是矩形
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个多边形的内角和等于900°,则这个多边形的边数是_____.
相关试题

