【题目】如图所示,有若干边长为1的正方形卡片,第1次并排摆2张黑色卡片,铺成一个长方形;第2次在黑色卡片上方和右侧摆白色卡片,所有卡片铺成了一个较大的长方形;第3次继续在白色卡片上方和右侧摆黑色卡片,所有卡片铺成了一个更大的长方形;以此类推,请解决以下问题:
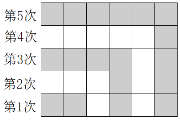
(1)仅第10次要用去______张卡片,摆完第10次后,总共用去_______张卡片.
(2)你知道 2+4+6+8+……+2n的结果是多少吗?写出结果,结合图形规律说明你的理由.
(3)求出从第51次至第100次所摆卡片的数量之和.
参考答案:
【答案】(1)20,110;(2)2+4+6+8+……+2n= n(n+1);(3)从第51次至第100次所摆卡片的数量之和7550.
【解析】
(1)观察图形可知:第1次共用去卡片2张,可以看成水平方向1张,竖直方向1张;第2次共用去卡片4张,可以看成水平方向2张,竖直方向2张;依次类推,可得:第n次共用去卡片2n张,可以看成水平方向n张,竖直方向n张.由此得到第10次共用去卡片20张,前10次共用去的卡片=2(1+2+3+……+9+10),计算即可.
(2)根据2+4+6+8+……+2n表示摆完第n次后共用去的卡片数.由图形可知:这些卡片共有n(n+1)张,即可得到结论;
(3) 用前100次用去的卡片数-前50次共用去的卡片数即可得到结论.
(1)观察图形可知:第1次共用去卡片2张,可以看成水平方向1张,竖直方向1张;
第2次共用去卡片4张,可以看成水平方向2张,竖直方向2张;
第3次共用去卡片6张,可以看成水平方向3张,竖直方向3张;
……
第n次共用去卡片2n张,可以看成水平方向n张,竖直方向n张.
由此得到第10次共用去卡片20张,前10次共用去卡片=2(1+2+3+……+9+10)=![]() =110.
=110.
故答案为:20,110.
(2)2+4+6+8+……+2n=n(n+1).
因为2+4+6+8+……+2n表示摆完第n次后共用去的卡片数.
根据图形可知:这些卡片共有n(n+1)张,
所以2+4+6+8+……+2n= n(n+1).
(3) 摆完第50次共用去50×(50+1)块卡片;
摆完第100次共用去100×(100+1)块卡片;
从第51次至第100次所摆卡片的数量之和为:
100×(100+1)-50×(50+1)=7550.
答:从第51次至第100次所摆卡片的数量之和7550.
-
科目: 来源: 题型:
查看答案和解析>>【题目】彩虹服装店用
 元购进
元购进 件衬衣,很快全部售完.服装店老板以每件
件衬衣,很快全部售完.服装店老板以每件 元的价格为标准,将超出的记为正数,不足的记为负数,记录如下:
元的价格为标准,将超出的记为正数,不足的记为负数,记录如下: ,
, ,
, ,
, ,
, ,
, ,
, ,
, (单位:元).他卖完这
(单位:元).他卖完这 件衬衣后是盈利还是亏损?盈利(或亏损)了多少钱?
件衬衣后是盈利还是亏损?盈利(或亏损)了多少钱? -
科目: 来源: 题型:
查看答案和解析>>【题目】一天早晨,乐乐以80米/分的速度上学,5分钟后乐乐的爸爸发现他忘了带数学书,爸爸立即骑自行车以280米/分的速度去追乐乐,并且在途中追上了他,请解决以下问题:
(1)爸爸追上乐乐用了多长时间?
(2)爸爸追上乐乐后,乐乐搭爸爸的自行车回到学校,结果提前了10分钟到校,若爸爸搭上乐乐后的骑行速度为240米/分,求乐乐家离学校有多远.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,点E为BC边上一点,AE和BD交于点F,已知△ABF的面积等于 6,△BEF的面积等于4,则四边形CDFE的面积等于___________

-
科目: 来源: 题型:
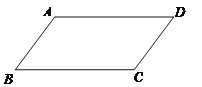
查看答案和解析>>【题目】如图,已知AD∥BC,要使四边形ABCD为平行四边形,需要增加的一个条是:_____.(只填一个你认为正确的条件即可,不添加任何线段与字母)
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了应对人口老龄化问题,国家大力发展养老事业.某养老机构定制轮椅供行动不便的老人使用.图①是一种型号的手动轮椅实物图,图②为其侧面示意图,该轮椅前后长度为120cm,后轮半径为24cm,CB=CD=24cm,踏板CB与CD垂直,横档AD、踏板CB与地面所成的角分别为15°、30°.求:
(1)求横档AD的长;
(2)点C离地面的高度.(sin15°=0.26,cos15°=0.97,精确到1cm)

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:∠AOB=90°,∠COD=20°,OM平分∠AOC,ON平分∠BOD.
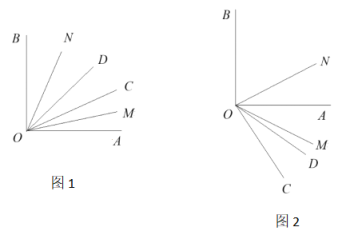
(1)如图1,∠COD在∠AOB内部,且∠AOC=30°.则∠MON的大小为 .
(2)如图1,∠COD在∠AOB内部,若∠AOC的度数未知,是否能求出∠MON的大小,若能,写出你的解答过程;若不能,说明理由.
(3)如图2,∠COD在∠AOB外部(OM在OD上方,∠BOC
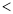 180°),试求出∠MON的大小.
180°),试求出∠MON的大小.
相关试题

