【题目】如图,在Rt△ABC中,∠ACB=90°,BD是∠ABC的平分线,点O在AB上,⊙O经过B,D两点,交BC于点E.
(1)求证:AC是⊙O的切线;
(2)若AB=6,sin∠BAC=![]() ,求BE的长.
,求BE的长.

参考答案:
【答案】(1)证明见解析;(2)3.2.
【解析】试题分析:(1)连接DO,由等腰三角形的性质和角平分线的定义得出∠1=∠3,证出DO∥BC,由平行线的性质得出∠ADO=90°,即可得出结论;
(2)设⊙O的半径为R,由三角函数求出BC,由平行线得出△AOD∽△ABC,得出对应边成比例,求出半径OD,过O作OF⊥BC于F,则BE=2BF,如图所示:则OF∥AC,由平行线的性质得出∠BOF=∠BAC,由三角函数求出BF,即可得出结果.
试题解析:(1)连接DO,如图1所示
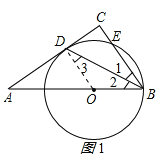
∵BD是∠ABC的平分线,
∴∠1=∠2,
∵OB=OD,
∴∠2=∠3,
∴∠1=∠3,
∴DO∥BC,
∵∠C=90°,
∴∠ADO=90°,
即AC⊥OD,
∴AC是⊙O的切线.
(2)设⊙O的半径为R,
在Rt△ABC中,∠ACB=90°,sin∠BAC=![]() ,
,
∴BC=![]() ×6=4,
×6=4,
由(1)知,OD∥BC,
∴△AOD∽△ABC,
∴![]() ,
,
∴![]() ,
,
解得:R=2.4,
过O作OF⊥BC于F,如图所示:
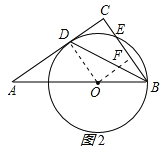
则BE=2BF,OF∥AC,
∴∠BOF=∠BAC,
∴![]() sin∠BOF=
sin∠BOF=![]() ,
,
∴BF=![]() ×2.4=1.6,
×2.4=1.6,
∴BE=2BF=3.2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】餐桌边的一蔬一饭,舌尖上的一饮一酌,实属来之不易,舌尖上的浪费让人触目惊心.据统计,中国每年浪费的食物总量折合粮食约500亿千克,这个数据用科学记数法表示为( )
A.5×1010千克 B.50×109千克 C.5×109千克 D.0.5×1011千克
-
科目: 来源: 题型:
查看答案和解析>>【题目】记M(1)=﹣2,M(2)=(﹣2)×(﹣2),M(3)=(﹣2)×(﹣2)×(﹣2),…,M(n)=

(1)填空:M(5)= , M(50) 是一个数(填“正”或“负”)
(2)计算:①2M(6)+M(7);②4M(7)+2M(8);
(3)直接写出2016M(n)+1008M(n+1)的值为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】方程2x﹣1=﹣5的解是( )
A. 3 B. ﹣3 C. 2 D. ﹣2
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.a2a3=a6B.a6÷a3=a2C.(ab)2=ab2D.(﹣a2)3=﹣a6
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据给出的数轴及已知条件,解答下面的问题:

(1)已知点A,B,C表示的数分别为1,﹣ ,﹣3观察数轴,与点A的距离为3的点表示的数是 , B,C两点之间的距离为;
,﹣3观察数轴,与点A的距离为3的点表示的数是 , B,C两点之间的距离为;
(2)若将数轴折叠,使得A点与C点重合,则与B点重合的点表示的数是;若此数轴上M,N两点之间的距离为2015(M在N的左侧),且当A点与C点重合时,M点与N点也恰好重合,则M,N两点表示的数分别是:M , N;
(3)若数轴上P,Q两点间的距离为m(P在Q左侧),表示数n的点到P,Q两点的距离相等,则将数轴折叠,使得P点与Q点重合时,P,Q两点表示的数分别为:P , Q(用含m,n的式子表示这两个数). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知A、B两地相距40km,甲、乙两人沿同一公路从A地出发到B地,甲骑摩托车,乙骑自行车,图中CD、OE分别表示甲、乙离开A地的路程y(km)与时间x(h)的函数关系的图象,结合图象解答下列问题.
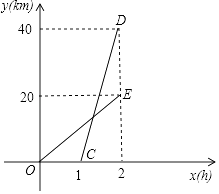
(1)甲比乙晚出发小时,乙的速度是km/h;
(2)在甲出发后几小时,两人相遇?
(3)甲到达B地后,原地休息0.5小时,从B地以原来的速度和路线返回A地,求甲在返回过程中与乙相距10km时,对应x的值.
相关试题

