【题目】如图,△ABC是等边三角形,边长为5,D为AC边上一动点,连接BD,⊙O为△ABD的外接圆,过点A作AE∥BC交⊙O于E,连接DE,则△BDE的面积的最小值为 . 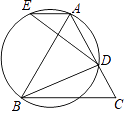
参考答案:
【答案】![]()
【解析】解:如图所示:连接BE, 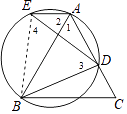
∵等边三角形ABC,
∴∠1=∠C=60°,
∵AE∥BC,
∴∠CAE+∠C=180°,
∴∠CAE=∠1+∠2=180°﹣∠C=120°,
∴∠1=∠2=60°,
∵∠1=4;∠2=∠3(同弧圆周角相等),
∴∠3=∠4=∠1=∠2=60°,
∴△BDE是等边三角形;
当⊙O的半径最小时△BDE的面积的最小,当AB是⊙O的直径时,⊙O的半径最小= ![]() AB=
AB= ![]() ,
,
此时BD⊥AC,
∴DE=BD=ABsin∠1=5× ![]() =
= ![]() ,
,
∴△BDE的面积的最小值= ![]() ×
× ![]() ×
× ![]() ×
× ![]() =
= ![]() .
.
所以答案是 ![]() .
.
【考点精析】掌握等边三角形的性质和三角形的外接圆与外心是解答本题的根本,需要知道等边三角形的三个角都相等并且每个角都是60°;过三角形的三个顶点的圆叫做三角形的外接圆,其圆心叫做三角形的外心.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将抛物线y=﹣2x2﹣1向上平移若干个单位,使抛物线与坐标轴有三个交点,如果这些交点能够成等边三角形,那么平移的距离为( )
A.1个单位
B.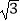 个单位
个单位
C. 个单位
个单位
D. 个单位
个单位 -
科目: 来源: 题型:
查看答案和解析>>【题目】请从以下两个小题中任选一个作答,若多选,则按所选的第一题计分.
A.如图,DE为△ABC的中位线,点F为DE上一点,且∠AFB=90°,若AB=8,BC=10,则EF的长为 .
B.小智同学在距大雁塔塔底水平距离为138米处,看塔顶的仰角为24.8(不考虑身高因素),则大雁塔市约为米.(结果精确到0.1米)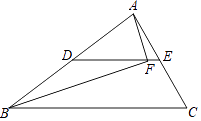
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC(网格中每个小正方形的边长均为1).
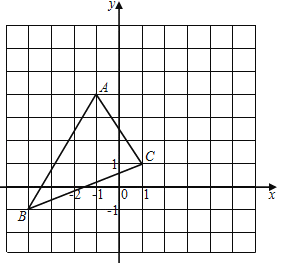
(1)三个顶点坐标分别为:A ,B ,C ;
(2)求三角形ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
 市首批一次性投放公共自行车700辆供市民租用出行,由于投入数量不够, 导致出现需要租用却未租到车的现象,现随机抽取的某五天在同一时段的调查数据汇成如下表格.
市首批一次性投放公共自行车700辆供市民租用出行,由于投入数量不够, 导致出现需要租用却未租到车的现象,现随机抽取的某五天在同一时段的调查数据汇成如下表格.请回答下列问题:
时间
第一天7:00﹣8:00
第二天7:00﹣8:00
第三天7:00﹣8:00
第四天7:00﹣8:00
第五天7:00﹣8:00
需要租用自行车却未租到车的人数(人)
1500
1200
1300
1300
1200
(1)表格中的五个数据(人数)的中位数是多少?
(2)由随机抽样估计,平均每天在7:00-8:00 :需要租用公共自行车的人数是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某体育老师测量了自己任教的甲、乙两班男生的身高,并制作了如下不完整的统计图表
身高分组
频数
频率
152≤ x<155
3
0.06
155≤ x<158
7
0.14
158≤ x<161
m
0.28
161≤ x<164
13
n
164≤ x<167
9
0.18
167≤ x<170
3
0.06
170≤ x<173
1
0.02

根据以上统计图表完成下列问题:
(1)统计表中m=____,n=____;并将频数分布直方图补充完整;
(2)在这次测量中两班男生身高的中位数在什么范围内?
相关试题

