【题目】如图,O是直线AB上一点,OC为任意一条射线,OD平分∠BOC,OE平分∠AOC.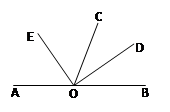
(1)指出图中∠AOD与∠BOE的补角;
(2)试判断∠COD与∠COE具有怎样的数量关系.并说明理由.
参考答案:
【答案】
(1)解:因为∠AOD+∠BOD=180,
所以∠AOD的补角为∠BOD,
又因为OD平分∠BOC,
所以∠COD=∠BOD,
所以∠AOD的补角为∠BOD,∠COD;
同理因为∠AOE+∠BOE=180,
所以∠BOE的补角为∠AOE,
又因为OE平分∠AOC,
所以∠COE=∠AOE,
所以∠BOE的补角为∠AOE,∠COE
(2)解:∵OD平分∠BOC,OE平分∠AOC,
∴∠COE= ![]() ∠AOC,∠COD=
∠AOC,∠COD= ![]() ∠BOC,
∠BOC,
∴∠COD+∠COE= ![]() ∠BOC+
∠BOC+ ![]() ∠AOC=
∠AOC= ![]() ∠AOB=90,
∠AOB=90,
即∠COD与∠COE的数量关系是∠COD+∠COE=90
【解析】 (1)根据已知和图形可知∠AOD+∠BOD=180,∠AOE+∠BOE=180,再根据角平分线的定义得出∠COD=∠BOD,∠COE=∠AOE,即可得出图中∠AOD与∠BOE的补角。
(2)根据角平分线的定义,可得出∠COE与∠AOC的数量关系,∠COD与∠BOC的数量关系,再求出∠COD与∠COE的和,即可得出结论。
-
科目: 来源: 题型:
查看答案和解析>>【题目】若△ABC和△DEF的面积分别为S1、S2 .
(1)如图①,AC=DF,BC=DE,∠C=30°,∠D=150°,比较S1与S2的大小为;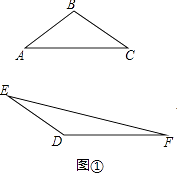
A.S1>S2
B.S1<S2
C.S1=S2
D.不能确定
(2)说明(1)的理由.
(3)如图②,在△ABC与△DEF中,AC=DF,BC=DE,∠C=30°,点E在以D为圆心,DE长为半径的半圆上运动,∠EDF的度数为α,比较S1与S2的大小(直接写出结果,不用说明理由).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:抛物线y=x2+bx+c经过点(2,-3)和(4,5)。

(1)求抛物线的表达式及顶点坐标;
(2)将抛物线沿x轴翻折,得到图象G,求图象G的表达式;
(3)在(2)的条件下,当-2<x<2时,直线y=m与该图象有一个公共点,求m的值或取值范围。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某文具店购进一批纪念册,每本进价为20元,出于营销考虑,要求每本纪念册的售价不低于20元且不高于28元,在销售过程中发现该纪念册每周的销售量y(本)与每本纪念册的售价x(元)之间满足一次函数关系:当销售单价为22元时,销售量为36本;当销售单价为24元时,销售量为32本.
(1)请直接写出y与x的函数关系式;
(2)当文具店每周销售这种纪念册获得150元的利润时,每本纪念册的销售单价是多少元?
(3)设该文具店每周销售这种纪念册所获得的利润为w元,将该纪念册销售单价定为多少元时,才能使文具店销售该纪念册所获利润最大?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD和正方形OEFG中,点A和点F的坐标分别为 (3,2),(-1,-1),则两个正方形的位似中心的坐标是( )

A.(1,0)
B.(-5,-1)
C.(1,0)或(-5,-1)
D.(1,0)或(-5,-2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式中,不含因式a+1的是( )
A.a2﹣1
B.2a2+4a+2
C.a2+a﹣2
D.a2﹣2a﹣3 -
科目: 来源: 题型:
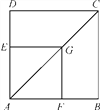
查看答案和解析>>【题目】如图,G是正方形ABCD对角线AC上一点,作GE⊥AD,GF⊥AB,垂足分别为点E、F.
求证:四边形AFGE与四边形ABCD相似.
相关试题

