【题目】如图,菱形ABCD的周长为16,若![]() ,E是AB的中点,则点E的坐标为_____________.
,E是AB的中点,则点E的坐标为_____________.

参考答案:
【答案】![]()
【解析】首先求出AB的长,进而得出EO的长,再利用锐角三角函数关系求出E点横纵坐标即可.
解:如图所示,过E作EM⊥AC,
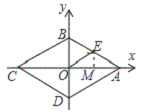
已知四边形ABCD是菱形,且周长为16,∠BAD=60°,根据菱形的性质可得AB=CD-BC=AD=4,AC⊥DB,∠BAO=![]() ∠BAD=30°,又因E是AB的中点,根据直角三角形中,斜边的中线等于斜边的一半可得EO=EA=EB=
∠BAD=30°,又因E是AB的中点,根据直角三角形中,斜边的中线等于斜边的一半可得EO=EA=EB=![]() AB=2,根据等腰三角形的性质可得∠BAO=∠EOA=30°,由直角三角形中,30°的锐角所对的直角边等于斜边的一半可得EM=
AB=2,根据等腰三角形的性质可得∠BAO=∠EOA=30°,由直角三角形中,30°的锐角所对的直角边等于斜边的一半可得EM=![]() OE=1,在Rt△OME中,由勾股定理可得OM=
OE=1,在Rt△OME中,由勾股定理可得OM=![]() ,所以点E的坐标为(
,所以点E的坐标为(![]() ,1),
,1),
故选B.
“点睛”此题主要考查了菱形的性质以及锐角三角函数关系应用,根据已知得出EO的长以及∠EOA=∠EAO=30°是解题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】A、B 两个码头相距800km,现有甲、乙两艘轮船分别以40km/h,60km/h 的速度从A、B 两地同时相向而行.已知轮船从A 码头开往B码头顺流航行.设水流的速度为a km/h,则:
(1)甲轮船在静水中的速度为__________km/h,乙轮船在静水中的速度为____________km/h;
(2)多少小时后甲、乙两艘轮船相距100km?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知等腰Rt△ABC中,AB=AC,∠BAC=
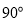 ,点A、B分别在x轴和y轴上,点C的坐标为(6,2).
,点A、B分别在x轴和y轴上,点C的坐标为(6,2).(1)如图1,求A点坐标;
(2)如图2,延长CA至点D,使得AD=AC,连接BD,线段BD交x轴于点E,问:在x轴上是否存在点M,使得△BDM的面积等于△ABO的面积,若存在,求点M的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】市自来水公司为鼓励用户节约用水,按以下规定收取水费:月用水量不超过40吨,每吨收费1元,另每吨水费加收0.2元的城市污水处理费,超过40吨的部分,每吨加收费用0.5元.
(1)某用户1月份共交水费65元,该用户1 月份用水多少吨?
(2)该用户2月份水表出现故障,每次用水只有60%计入用水量,这样2月份交水费43.2元,该用户2 月份实际应交水费多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,AB=18,cosB=
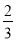 ,把△ABC绕着点C旋转,使点B与AB边上的点D重合,点A落在点E处,则线段AE的长为( )
,把△ABC绕着点C旋转,使点B与AB边上的点D重合,点A落在点E处,则线段AE的长为( )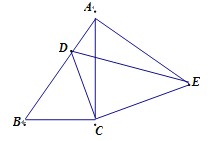
A. 6
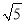 B. 7
B. 7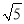 C. 8
C. 8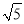 D. 9
D. 9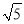
-
科目: 来源: 题型:
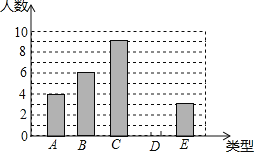
查看答案和解析>>【题目】某单位750名职工积极参加向贫困地区学校捐书活动,为了解职工的捐数量,采用随机抽样的方法抽取30名职工作为样本,对他们的捐书量进行统计,统计结果共有4本、5本、6本、7本、8本五类,分别用A、B、C、D、E表示,根据统计数据绘制成了如图所示的不完整的条形统计图,由图中给出的信息解答下列问题:
(1)补全条形统计图;
(2)求这30名职工捐书本数的平均数、众数和中位数;
(3)估计该单位750名职工共捐书多少本?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=-
 x-
x-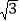 与x,y两轴分别交于A,B两点,与反比例函数y=
与x,y两轴分别交于A,B两点,与反比例函数y= 的图象在第二象限交于点C.过点A作x轴的垂线交该反比例函数图象于点D.若AD=AC,则点D的纵坐标为___.
的图象在第二象限交于点C.过点A作x轴的垂线交该反比例函数图象于点D.若AD=AC,则点D的纵坐标为___.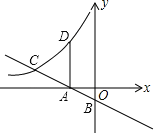
相关试题

