搜索
【题目】为实现教育均衡发展，打造新优质学校，瑶海区计划对A、B两类薄弱学校全部进行改造，根据预算，共需资金1575万元．改造一所A类学校和两所B类学校共需资金230万元；改造两所A类学校和一所B类学校共需资金205万元，求改造一所A类学校和一所B类学校所需的资金分别是多少万元？
参考答案：
【答案】改造一所A类学校所需资金为60万元，改造一所B类学校所需的资金是85万元．
【解析】
试题设改造一所A类学校所需资金为x万元，改造一所B类学校所需的资金是y万元，根据改造一所A类学校和两所B类学校共需资金230万元；改造两所A类学校和一所B类学校共需资金205万元，列方程组求解．
解：设改造一所A类学校所需资金为x万元，改造一所B类学校所需的资金是y万元，
由题意得，
，
解得：
．
答：改造一所A类学校所需资金为60万元，改造一所B类学校所需的资金是85万元．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AB为⊙O的直径，点C在⊙O上，点P是直径AB上的一点（不与A重合），过点P作AB的垂线交BC于点Q．
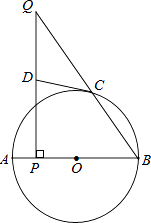
（1）在线段PQ上取一点D，使DQ=DC，连接DC，试判断CD与⊙O的位置关系，并说明理由．
（2）若cosB=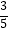
，BP=6，AP=1，求QC的长． -
科目： 来源： 题型：
查看答案和解析>>【题目】在等腰△ABC中，AC=BC，以BC为直径的⊙O分别与AB，AC相交于点D，E，过点D作DF⊥AC，垂足为点F．
（1）求证：DF是⊙O的切线；
（2）分别延长CB，FD，相交于点G，∠A=60°，⊙O的半径为6，求阴影部分的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知，点O是直线AB上一点，OC、OD为从点O引出的两条射线，∠BOD=30°，∠COD=
∠AOC．（1）如图①，求∠AOC的度数；
（2）如图②，在∠AOD的内部作∠MON=90°，请直接写出∠AON与∠COM之间的数量关系 ；
（3）在（2）的条件下，若OM为∠BOC的角平分线，试说明∠AON=∠CON．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，A、B两地相距200km，一列火车从B地出发沿BC方向以
的速度行驶，在行驶过程中，这列火车离A地的路程
与行驶时间
之间的函数关系式是______．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在汶川地震十周年纪念日，某教育集团进行了主题捐书活动，同学们热情高涨，仅仅五天就捐赠图书m万册，其中m与
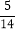互为倒数．此时教育集团决定把所捐图书分批次运往市区周边的“希望学校”，而捐书活动将再持续一周．下表为活动结束前一周所捐图书存量的增减变化情况（单位：万册）：第一天
第二天
第三天
第四天
第五天
第六天
第七天
+0.2
+0.1
﹣0.1
﹣0.4
+0.3
+0.5
﹣0.1
（1）m的值为 ．
（2）求活动结束时，该教育集团所捐图书存量为多少万册；
（3）活动结束后，该教育集团决定在6天内把所捐图书全部运往“希望学校”，现有A、B两个运输公司，B运输公司每天的运输数量是A运输公司的1.5倍，学校首先聘请A运输公司进行运输，工作两天后，由于某些原因，A运输公司每天运输的数量比原来降低了25%，学校决定又聘请B运输公司加入，与A运输公司共同运输，恰好按时完成任务，求A运输公司每天运输多少万册图书？
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图，在△ABC中，∠C=90°，∠BAC的平分线AD交BC于点D，过点D作DE⊥AD交AB于点E，以AE为直径作⊙O．
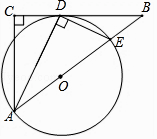
（1）求证：BC是⊙O的切线；
（2）若AC=3，BC=4，求BE的长．
相关试题
