【题目】已知:如图,ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E. 
(1)求证:△AOD≌△EOC;
(2)连接AC,DE,当∠B=∠AEB=°时,四边形ACED是正方形?请说明理由.
参考答案:
【答案】
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC.
∴∠D=∠OCE,∠DAO=∠E.
∵O是CD的中点,
∴OC=OD,
在△ADO和△ECO中,
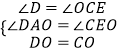 ,
,
∴△AOD≌△EOC(AAS);
(2)45
【解析】(2)当∠B=∠AEB=45°时,四边形ACED是正方形. ∵△AOD≌△EOC,
∴OA=OE.
又∵OC=OD,
∴四边形ACED是平行四边形.
∵∠B=∠AEB=45°,
∴AB=AE,∠BAE=90°.
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∴∠COE=∠BAE=90°.
∴ACED是菱形.
∵AB=AE,AB=CD,
∴AE=CD.
∴菱形ACED是正方形.
所以答案是:45.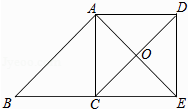
【考点精析】根据题目的已知条件,利用平行四边形的性质和正方形的判定方法的相关知识可以得到问题的答案,需要掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;先判定一个四边形是矩形,再判定出有一组邻边相等;先判定一个四边形是菱形,再判定出有一个角是直角.
-
科目: 来源: 题型:
查看答案和解析>>【题目】回答下列问题:
(1)如图所示的甲、乙两个平面图形能折什么几何体?

(2)由多个平面围成的几何体叫做多面体.若一个多面体的面数为f,顶点个数为v,棱数为e,分别计算第(1)题中两个多面体的f+v﹣e的值?你发现什么规律?
(3)应用上述规律解决问题:一个多面体的顶点数比面数大8,且有50条棱,求这个几何体的面数.
-
科目: 来源: 题型:
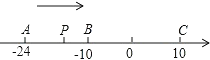
查看答案和解析>>【题目】已知数轴上有A,B,C三个点,分别表示有理数﹣24,﹣10,10,动点P从A出发,以每秒1个单位的速度向终点C移动,设移动时间为t秒.
(1)用含t的代数式表示P到点A和点C的距离:
PA=________,PC=________;
(2)当点P运动到B点时,点Q从A点出发,以每秒3个单位的速度向C点运动,Q点到达C点后,再立即以同样的速度返回,运动到终点A.在点Q开始运动后,P,Q两点之间的距离能否为2个单位?如果能,请求出此时点P表示的数;如果不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2016年G20杭州峰会期间,某志愿者小组有五名翻译,其中一名只会翻译法语,三名只会翻译英语,还有一名两种语言都会翻译.若从中随机挑选两名组成一组,则该组能够翻译上述两种语言的概率是多少?(请用“画树状图”的方法给出分析过程,并求出结果)
-
科目: 来源: 题型:
查看答案和解析>>【题目】解答下列各题
(1)化简并求值:-(3a2-4ab)+[a2-
 (a+2ab)] ,其中a=-2,b=1
(a+2ab)] ,其中a=-2,b=1 (2)已知多项式(2x2+ax-y+6)-(2bx2-3x+5y-1)的值与字母x的取值无关,求a、b的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了创建全国卫生城市,某社区要清理一个卫生死角内的垃圾,租用甲、乙两车运送,两车各运12趟可完成,需支付运费4800元.已知甲、乙两车单独运完此堆垃圾,乙车所运趟数是甲车的2倍,且乙车每趟运费比甲车少200元.
(1)求甲、乙两车单独运完此堆垃圾各需运多少趟?
(2)若单独租用一台车,租用哪台车合算? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,梯子斜靠在与地面垂直(垂足为O)的墙上,当梯子位于AB位置时,它与地面所成的角∠ABO=60°;当梯子底端向右滑动1m(即BD=1m)到达CD位置时,它与地面所成的角∠CDO=51°18′,求梯子的长. (参考数据:sin51°18′≈0.780,cos51°18′≈0.625,tan51°18′≈1.248)

相关试题

