【题目】如图,已知线段AB,CD相交于点O,AD,CB的延长线交于点E,OA=OC,EA=EC.
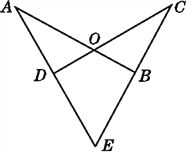
(1)试说明:∠A=∠C;
(2)在(1)的解答过程中,需要作辅助线,它的意图是什么?
参考答案:
【答案】(1)见解析;(2)构造全等三角形.
【解析】分析:(1)根据题意,没有证明两三角形全等的条件,所以要作条辅助线,连接OE;然后就可以利用SSS全等判定定理证明两三角形全等,继而∠A=∠C,本题即可证明(1),(2),说明OE的意义即可.
本题解析:
(1)如图,连接OE.
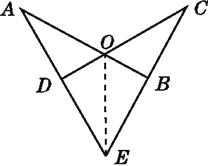
在△EAO和△ECO中, 
所以△EAO≌△ECO(SSS).
所以∠A=∠C(全等三角形的对应角相等).
(2)构造全等三角形.
意图:本题运用了构造法,通过连接OE,构造△OAE,△OCE,将欲说明相等的∠A,∠C分别置于这两个三角形中,然后通过说明全等可得∠A=∠C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(4,3),AB∥x轴,且AB=4,则点B的坐标为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】3的相反数是( )
A.0B.3C.-3D.6
-
科目: 来源: 题型:
查看答案和解析>>【题目】一件商品的进价为a元,将进价提高100%后标价,再按标价打七折销售,则这件商品销售后的利润为 元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BC⊥AC,BC=8,AC=6,AB=10,则点 C 到线段 AB 的距离是_____.
[Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/4/13/1923292236627968/1924724835434496/STEM/46ca9c8351da4594816ea507a60c9cdd.png]
-
科目: 来源: 题型:
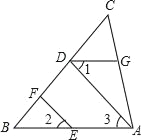
查看答案和解析>>【题目】如图,已知点D、F、E、G都在△ABC的边上,EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.(请在下面的空格处填写理由或数学式)
解:∵EF∥AD,(已知)
∴∠2= ( )
∵∠1=∠2,(已知)
∴∠1= ( )
∴ ∥ ,( )
∴∠AGD+ =180°,(两直线平行,同旁内角互补)
∵ ,(已知)
∴∠AGD= (等式性质)
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线AB、CD相交于点O,OE平分∠BOD,OF⊥CD,垂足为O.
(1)若∠EOF=54°,求∠AOC的度数;
(2)①在∠AOD的内部作射线OG⊥OE;
②试探索∠AOG与∠EOF之间有怎样的关系?并说明理由.

相关试题

