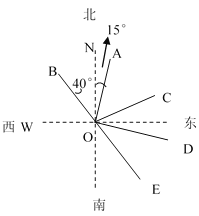
【题目】如图,射线OA的方向是北偏东15°,射线OB的方向是北偏西40°,∠AOB=∠AOC,射线OE是射线OB的反向延长线.
(1)求射线OC的方向角;
(2)求∠COE的度数;
(3)若射线OD平分∠COE,求∠AOD的度数.
参考答案:
【答案】(1)射线OC的方向是北偏东![]() °;(2)∠COE=
°;(2)∠COE=![]() °;(3)∠AOD=
°;(3)∠AOD=![]() °.
°.
【解析】
(1)先求出∠AOC=55°,再求得∠NOC的度数,即可确定OC的方向;
(2)根据∠AOC=55°,∠AOC=∠AOB,得出∠BOC=110°,进而求出∠COE的度数;
(3)根据射线OD平分∠COE,即可求出∠COD=35°再利用∠AOC=55°求出答案即可.
(1)∵射线OA的方向是北偏东![]() °,射线OB的方向是北偏西
°,射线OB的方向是北偏西![]() °
°
即∠NOA=![]() °,∠NOB=
°,∠NOB=![]() °,
°,
∴∠AOB=∠NOA+∠NOB=![]() °,
°,
又∵∠AOB=∠AOC,
∴∠AOC=![]() °,
°,
∴∠NOC=∠NOA+∠AOC=![]() °+
°+ ![]() °
°![]() °,
°,
∴射线OC的方向是北偏东![]() °.
°.
(2)∵∠AOB=![]() °,∠AOB=∠AOC,
°,∠AOB=∠AOC,
∴∠BOC=∠AOB+∠AOC=![]() °+
°+![]() °=
°=![]() °,
°,
又∵射线OD是OB的反向延长线,
∴∠BOE=![]() °,
°,
∴∠COE=![]() °-
°-![]() °=
°=![]() °,
°,
(3)∵∠COE=![]() °,OD平分∠COE,
°,OD平分∠COE,
∴∠COD=![]() °,
°,
∴∠AOD=∠AOC+∠COD=![]() °+
°+![]() °=
°=![]() °.
°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2017浙江省湖州市,第23题,10分)湖州素有鱼米之乡之称,某水产养殖大户为了更好地发挥技术优势,一次性收购了20000kg淡水鱼,计划养殖一段时间后再出售.已知每天放养的费用相同,放养10天的总成本为30.4万元;放养20天的总成本为30.8万元(总成本=放养总费用+收购成本).
(1)设每天的放养费用是a万元,收购成本为b万元,求a和b的值;
(2)设这批淡水鱼放养t天后的质量为m(kg),销售单价为y元/kg.根据以往经验可知:m与t的函数关系为
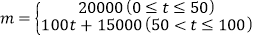 ;y与t的函数关系如图所示.
;y与t的函数关系如图所示.①分别求出当0≤t≤50和50<t≤100时,y与t的函数关系式;
②设将这批淡水鱼放养t天后一次性出售所得利润为W元,求当t为何值时,W最大?并求出最大值.(利润=销售总额﹣总成本)

-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形ABCD的边长为6cm,点E,M分别是线段BD,AD上的动点,连接AE并延长,交边BC于F,过M作MN⊥AF,垂足为H,交边AB于点N.
(1)如图①,若点M与点D重合,求证:AF=MN;
(2)如图②,若点M从点D出发,以1cm/s的速度沿DA向点A运动,同时点E从点B出发,以
 cm/s的速度沿BD向点D运动,运动时间为ts.
cm/s的速度沿BD向点D运动,运动时间为ts.①设BF=ycm,求y关于t的函数表达式;
②当BN=2AN时,连接FN,求FN的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,P点从点A开始以2厘米/秒的速度沿A→B→C的方向移动,点Q从点C开始以1厘米/秒的速度沿C→A→B的方向移动,在直角三角形ABC中,∠A=90°,若AB=16厘米,AC=12厘米,BC=20厘米,如果P、Q同时出发,用t(秒)表示移动时间,那么:
(1)如图1,若P在线段AB上运动,Q在线段CA上运动,试求出t为何值时,QA=AP
(2)如图2,点Q在CA上运动,试求出t为何值时,三角形QAB的面积等于三角形ABC面积的
 ;
;(3)如图3,当P点到达C点时,P、Q两点都停止运动,试求当t为何值时,线段AQ的长度等于线段BP的长的


-
科目: 来源: 题型:
查看答案和解析>>【题目】小明同学为了解自己居住的小区家庭生活用水情况,从中随机调查了其中
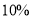 的家庭一年的月平均用水量(单位:顿).并将调查结果制成了如图所示的条形和扇形统计图.
的家庭一年的月平均用水量(单位:顿).并将调查结果制成了如图所示的条形和扇形统计图.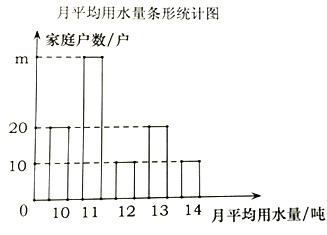
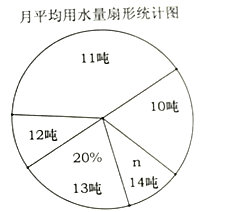
 小明随机调查了 户家庭,该小区共有 户家庭;
小明随机调查了 户家庭,该小区共有 户家庭;
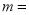 ,
,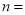 ;
;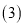 这个样本数据的众数是 ,中位数是 ;
这个样本数据的众数是 ,中位数是 ;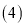 根据样本数据,请估计该小区家庭月平均用水量不超过
根据样本数据,请估计该小区家庭月平均用水量不超过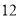 吨的有多少户?
吨的有多少户? -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学库存若干套桌椅,准备修理后支援贫困山区学校。现有甲、乙两木工组,甲每天修理桌椅16套,乙每天修桌椅比甲多8套,甲单独修完这些桌椅比乙单独修完多用20天,学校每天付甲组80元修理费,付乙组120元修理费。
(1)该中学库存多少套桌椅?
(2)在修理过程中,学校要派一名工人进行质量监督,学校负担他每天10元生活补助费,现有三种修理方案:a、由甲单独修理;b、由乙单独修理;c、甲、乙合作同时修理。你认为哪种方案省时又省钱?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,A是抛物线
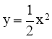 上的一个动点,且点A在第一象限内.AE⊥y轴于点E,点B坐标为(0,2),直线AB交
上的一个动点,且点A在第一象限内.AE⊥y轴于点E,点B坐标为(0,2),直线AB交 轴于点C,点D与点C关于y轴对称,直线DE与AB相交于点F,连结BD.设线段AE的长为m,△BED的面积为S.
轴于点C,点D与点C关于y轴对称,直线DE与AB相交于点F,连结BD.设线段AE的长为m,△BED的面积为S.(1)当
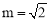 时,求S的值.
时,求S的值.(2)求S关于
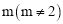 的函数解析式.
的函数解析式.(3)①若S=
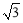 时,求
时,求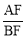 的值;
的值;②当m>2时,设
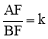 ,猜想k与m的数量关系并证明.
,猜想k与m的数量关系并证明.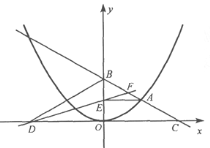
相关试题

