【题目】如图1,矩形ABCD的两条边在坐标轴上,点D与坐标原点O重合,且AD=8,AB=6.如图2,矩形ABCD沿OB方向以每秒1个单位长度的速度运动,同时点P从A点出发也以每秒1个单位长度的速度沿矩形ABCD的边AB经过点B向点C运动,当点P到达点C时,矩形ABCD和点P同时停止运动,设点P的运动时间为t秒.
(1)当t=5时,请直接写出点D、点P的坐标;
(2)当点P在线段AB或线段BC上运动时,求出△PBD的面积S关于t的函数关系式,并写出相应t的取值范围;
(3)点P在线段AB或线段BC上运动时,作PE⊥x轴,垂足为点E,当△PEO与△BCD相似时,求出相应的t值.

参考答案:
【答案】(1)D(﹣4,3),P(﹣12,8);(2)![]() ;(3)6.
;(3)6.
【解析】试题分析:(1)延长CD交x轴于M,延长BA交x轴于N,则CM⊥x轴,BN⊥x轴,AD∥x轴,BN∥DM,由矩形的性质得出和勾股定理求出BD,BO=15,由平行线得出△ABD∽△NBO,得出比例式![]() ,求出BN、NO,得出OM、DN、PN,即可得出点D、P的坐标;
,求出BN、NO,得出OM、DN、PN,即可得出点D、P的坐标;
(2)当点P在边AB上时,BP=6﹣t,由三角形的面积公式得出S=![]() BPAD;②当点P在边BC上时,BP=t﹣6,同理得出S=
BPAD;②当点P在边BC上时,BP=t﹣6,同理得出S=![]() BPAB;即可得出结果;
BPAB;即可得出结果;
(3)设点D(![]() ,
, ![]() );分两种情况:①当点P在边AB上时,P(
);分两种情况:①当点P在边AB上时,P(![]() ,
, ![]() ),由
),由![]() 和
和![]() 时;分别求出t的值;
时;分别求出t的值;
②当点P在边BC上时,P(![]() ,
, ![]() );由
);由![]() 和
和![]() 时,分别求出t的值即可.
时,分别求出t的值即可.
试题解析:(1)延长CD交x轴于M,延长BA交x轴于N,如图1所示:则CM⊥x轴,BN⊥x轴,AD∥x轴,BN∥DM,∵四边形ABCD是矩形,∴∠BAD=90°,CD=AB=6,BC=AD=8,∴BD=![]() =10,当t=5时,OD=5,∴BO=15,∵AD∥NO,∴△ABD∽△NBO,∴
=10,当t=5时,OD=5,∴BO=15,∵AD∥NO,∴△ABD∽△NBO,∴![]() ,即
,即![]() ,∴BN=9,NO=12,∴OM=12﹣8=4,DM=9﹣6=3,PN=9﹣1=8,/span>∴D(﹣4,3),P(﹣12,8);
,∴BN=9,NO=12,∴OM=12﹣8=4,DM=9﹣6=3,PN=9﹣1=8,/span>∴D(﹣4,3),P(﹣12,8);
(2)如图2所示:当点P在边AB上时,BP=6﹣t,∴S=![]() BPAD=
BPAD=![]() (6﹣t)×8=﹣4t+24;
(6﹣t)×8=﹣4t+24;
②当点P在边BC上时,BP=t﹣6,∴S=![]() BPAB=
BPAB=![]() (t﹣6)×6=3t﹣18;
(t﹣6)×6=3t﹣18;
综上所述: ![]() ;
;
(3)设点 D(![]() ,
, ![]() );
);
①当点P在边AB上时,P(![]() ,
, ![]() ),若
),若![]() 时,
时,  ,解得:t=6;
,解得:t=6;
若![]() 时,
时,  ,解得:t=20(不合题意,舍去);
,解得:t=20(不合题意,舍去);
②当点P在边BC上时,P(![]() ,
, ![]() ),若
),若![]() 时,
时,  ,解得:t=6;
,解得:t=6;
若![]() 时,
时,  ,解得:
,解得: ![]() (不合题意,舍去);
(不合题意,舍去);
综上所述:当t=6时,△PEO与△BCD相似.

-
科目: 来源: 题型:
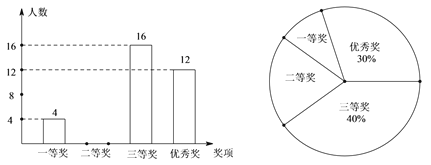
查看答案和解析>>【题目】某中学在全校学生中开展了“地球—我们的家园”为主题的环保征文比赛,评选出一、二、三等奖和优秀奖。根据奖项的情况绘制成如图所示的两幅不完整的统计图,请你根据图中提供的信息解答下列问题:
(1)求校获奖的总人数,并把条形统计图补充完整;
(2)求在扇形统计图中表示“二等奖” 的扇形的圆心角的度数;
(3)获得一等奖的4名学生中有3男1女,现打算从中随机选出2名学生参加颁奖活动,请用列表或画树状图的方法求选出的2名学生恰好是1男1女的概率﹒
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式(x﹣1)2﹣2(x﹣1)+1的结果是( )
A.(x﹣1)(x﹣2)
B.x2
C.(x+1)2
D.(x﹣2)2 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知2x﹣3y=3,则代数式6x﹣9y+5的值为
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店第一次用300元购进笔记本若干,第二次又用300元购进该款笔记本,但这次每本的进价是第一次进价的
 倍,购进数量比第一次少了25本.
倍,购进数量比第一次少了25本.(1)求第一次每本笔记本的进价是多少元?
(2)若要求这两次购进的笔记本按同一价格全部销售完毕后获利不低于450元,问每本笔记本的售价至少是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:2(x2y﹣xy2﹣1)﹣(2x2y﹣3xy2﹣3),其中x=2,y=﹣1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,已知△ABC是等腰直角三角形,∠BAC=90°,点D是BC的中点.作正方形DEFG,使点A,C分别在DG、DE上,连接AE、BG.
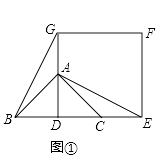
(1)试猜想线段BG和AE的数量关系,请直接写出你得到的结论;
(2)将正方形DEFG绕点D逆时针方向旋转一定角度后(旋转角度大于0°,小于或等于360°),如图②,(1)中的结论是否仍然成立?如果成立,请予以证明;如果不成立,请说明理由.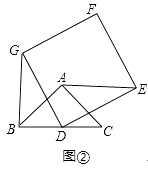
相关试题

