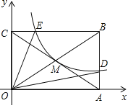
【题目】如图,反比例函数![]() 的图象经过矩形
的图象经过矩形![]() 对角线的交点
对角线的交点![]() ,分别与
,分别与![]() 、
、![]() 相交于点
相交于点![]() 、
、![]() .
.
(1)证明:![]() 与
与![]() 面积相等;
面积相等;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)若四边形![]() 面积为
面积为![]() ,求反比例函数的解析式.
,求反比例函数的解析式.
参考答案:
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)直接利用反比例函数的比例系数的几何意义直接回答即可;
(2)首先设出点E的坐标,然后表示出点B的坐标,根据反比例函数图象上点的坐标特征求出点D的坐标,进而求出BD:BA的值;
(3)设![]() 点坐标为
点坐标为![]() ,则
,则![]() ,即
,即![]() ,由点M为矩形OABC对角线的交点,根据矩形的性质易得
,由点M为矩形OABC对角线的交点,根据矩形的性质易得![]() ,
,![]() ,
,![]() ,利用坐标的表示方法得到D点的横坐标为2a,E点的纵坐标为2b,而点D、点E在反比例函数
,利用坐标的表示方法得到D点的横坐标为2a,E点的纵坐标为2b,而点D、点E在反比例函数![]() 的图象上,(即它们的横纵坐标之积为ab),可得
的图象上,(即它们的横纵坐标之积为ab),可得![]() 点的纵坐标为
点的纵坐标为![]() ,
,![]() 点的横坐标为
点的横坐标为![]() ,利用S矩形OABC=S△OAD+S△OCE+S四边形ODBE,得到
,利用S矩形OABC=S△OAD+S△OCE+S四边形ODBE,得到![]() ,求出ab,即可得到k的值.
,求出ab,即可得到k的值.
(1)∵四边形![]() 为矩形,
为矩形,
∴![]() ,
,![]() ,
,
∵![]() 、
、![]() 在反比例函数的图象上,
在反比例函数的图象上,
∴![]() ,
,
∴![]() 与
与![]() 面积相等;
面积相等;
(2)∵![]() ,
,
∴设点![]() 的坐标为
的坐标为![]() ,则点
,则点![]() 的坐标为
的坐标为![]() .
.
设点![]() 坐标为
坐标为![]() ,
,
∵![]() ,
,![]() 均在反比例函数
均在反比例函数![]() 的图象上,
的图象上,
∴![]() ,解得
,解得![]() .
.
∴![]() ,
,![]() ,
,
∴![]() .
.
(3)设![]() 点坐标为
点坐标为![]() ,则
,则![]() ,即
,即![]() ,
,
∵点![]() 为矩形
为矩形![]() 对角线的交点,
对角线的交点,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() 点的横坐标为
点的横坐标为![]() ,
,![]() 点的纵坐标为
点的纵坐标为![]() ,
,
又∵点![]() 、点
、点![]() 在反比例函数
在反比例函数![]() 的图象上,
的图象上,
∴![]() 点的纵坐标为
点的纵坐标为![]() ,
,![]() 点的横坐标为
点的横坐标为![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一个转盘,转盘被分成4个相同的扇形,颜色分为红、绿、黄三种,指针的位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,当作指向右边的扇形),求下列事件的概率:

(1)指针指向绿色;
(2)指针指向红色或黄色;
(3)指针不指向红色.
-
科目: 来源: 题型:
查看答案和解析>>【题目】春节前小王花1200元从农贸市场购进批发价分别为每箱30元与50元的A,B两种水果进行销售,并分别以每箱35元与60元的价格出售,设购进A水果x箱,B水果y箱.
(1)让小王将水果全部售出共赚了215元,则小王共购进A、B水果各多少箱?
(2)若要求购进A水果的数量不得少于B水果的数量,则应该如何分配购进A, B水果的数量并全部售出才能获得最大利润,此时最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
 交
交 轴于点
轴于点 ,过
,过 作
作 轴,双曲线
轴,双曲线 过
过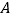 、
、 两点(
两点(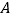 点在已知直线上),若
点在已知直线上),若 ,则
,则 ________.
________.
-
科目: 来源: 题型:
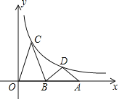
查看答案和解析>>【题目】如图,
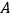 为
为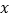 轴上一点,
轴上一点,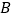 为
为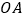 的中点,
的中点,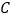 ,
,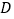 为反比例函数
为反比例函数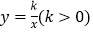 的图象上两点,且
的图象上两点,且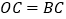 ,
,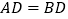 ,若
,若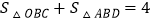 ,则
,则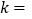 ________.
________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】双曲线
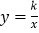 上一点
上一点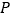 ,过
,过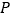 作
作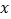 轴,
轴,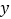 轴的垂线,垂足分别为
轴的垂线,垂足分别为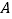 、
、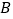 ,矩形
,矩形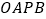 的面积为
的面积为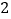 ,则双曲线与直线在
,则双曲线与直线在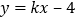 交点在第一象限内的点的坐标为________.
交点在第一象限内的点的坐标为________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△CEF中,∠C=90°,∠CEF, ∠CFE外角平分线交于点A,过点A分别作直线CE、CF的垂线,B、D为垂足.

(1)求证:四边形ABCD是正方形,
(2)已知AB的长为6,求(BE+6)(DF+6)的值,
(3)借助于上面问题的解题思路,解决下列问题:若三角形PQR中,∠QPR=45°,一条高是PH,长度为6,QH=2,则HR= .
相关试题

