【题目】如图1,在长方形ABCD中,AB=12cm,BC=10cm,点P从A出发,沿A→B→C→D的路线运动,到D停止;点Q从D点出发,沿D→C→B→A路线运动,到A点停止.若P、Q两点同时出发,速度分别为每秒lcm、2cm,a秒时P、Q两点同时改变速度,分别变为每秒2cm、![]() cm(P、Q两点速度改变后一直保持此速度,直到停止),如图2是△APD的面积s(cm2)和运动时间x(秒)的图象.
cm(P、Q两点速度改变后一直保持此速度,直到停止),如图2是△APD的面积s(cm2)和运动时间x(秒)的图象.
(1)求出a值;
(2)设点P已行的路程为y1(cm),点Q还剩的路程为y2(cm),请分别求出改变速度后,y1、y2和运动时间x(秒)的关系式;
(3)求P、Q两点都在BC边上,x为何值时P、Q两点相距3cm?

参考答案:
【答案】(1)6;(2)10或![]() ;
;
【解析】
(1)根据图象变化确定a秒时,P点位置,利用面积求a;
(2)P、Q两点的函数关系式都是在运动6秒的基础上得到的,因此注意在总时间内减去6秒;
(3)以(2)为基础可知,两个点相距3cm分为相遇前相距或相遇后相距,因此由(2)可列方程.
(1)由图象可知,当点P在BC上运动时,△APD的面积保持不变,则a秒时,点P在AB上.
![]() ,
,
∴AP=6,
则a=6;
(2)由(1)6秒后点P变速,则点P已行的路程为y1=6+2(x﹣6)=2x﹣6,
∵Q点路程总长为34cm,第6秒时已经走12cm,
故点Q还剩的路程为y2=34﹣12﹣![]() ;
;
(3)当P、Q两点相遇前相距3cm时,
![]() ﹣(2x﹣6)=3,解得x=10,
﹣(2x﹣6)=3,解得x=10,
当P、Q两点相遇后相距3cm时,
(2x﹣6)﹣(![]() )=3,解得x=
)=3,解得x=![]() ,
,
∴当x=10或![]() 时,P、Q两点相距3cm
时,P、Q两点相距3cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,已知
 是⊙
是⊙ 的直径,
的直径,  是
是 上的一个动点(点
上的一个动点(点 与点
与点 、
、 不重合),连接
不重合),连接 .
.  是
是 的中点,作弦
的中点,作弦 ,垂足为
,垂足为 .
.(
 )若点
)若点 和点
和点 不重合,连接
不重合,连接 、
、 和
和 .当
.当 是等腰三角形时,求
是等腰三角形时,求 的度数.
的度数.(
 )若点
)若点 和点
和点 重合,如图②.探索
重合,如图②.探索 与
与 的数量关系并说明理由.
的数量关系并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店销售甲、乙两种商品,现有如下信息:

请结合以上信息,解答下列问题:
(1)求甲、乙两种商品的进货单价;
(2)已知甲、乙两种商品的零售单价分别为2元、3元,该商店平均每天卖出甲商品500件和乙商品1300件,经市场调查发现,甲种商品零售单价每降0.1元,甲种商品每天可多销售100件,商店决定把甲种商品的零售单价下降m(m>0)元,在不考虑其他因素的条件下,求当m为何值时,商店每天销售甲、乙两种商品获取的总利润为1800元(注:单件利润=零售单价﹣进货单价)
-
科目: 来源: 题型:
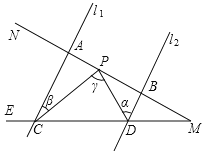
查看答案和解析>>【题目】如图,已知l1∥l2,射线MN分别和直线l1,l2交于A、B,射线ME分别和直线l1,l2交于C、D,点P在A、B间运动(P与A、B两点不重合),设∠PDB=α,∠PCA=β,∠CPD=γ.
(1)试探索α,β,γ之间有何数量关系?说明理由.
(2)如果BD=3,AB=9,AC=6,并且AC垂直于MN,那么点P运动到什么位置时,△ACP≌△BPD说明理由.
(3)在(2)的条件下,当△ACP≌△BPD时,PC与PD之间有何位置关系,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点
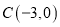 ,点
,点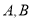 分别在
分别在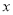 轴和
轴和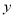 轴的正半轴上,且满足
轴的正半轴上,且满足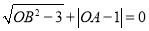 .
.(1)求点
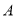 、点
、点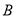 的坐标;
的坐标;(2)若点
 从点
从点 出发,以每秒1个单位长度的速度沿射线CB运动,连结AP,设
出发,以每秒1个单位长度的速度沿射线CB运动,连结AP,设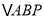 的面积为
的面积为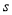 ,点
,点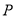 的运动时间为
的运动时间为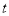 秒,求
秒,求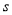 与
与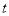 的函数关系式,并写出自变量
的函数关系式,并写出自变量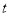 的取值范围;
的取值范围;(3)在(2)的条件下,是否存在点
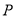 ,使得以点
,使得以点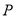 、
、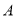 、
、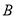 为顶点的三角形与
为顶点的三角形与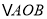 相似,若存在,请求出点
相似,若存在,请求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.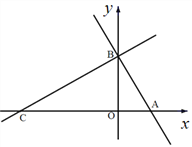
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD中,对角线AC、BD相交于点O,给出下列四组条件:①AB∥CD,AD∥BC;②AB=CD,AD=BC;③AO=CO,BO=DO;④AB∥CD,AD=BC。其中一定能判断这个四边形是平行四边形的条件共有
A. 1组 B. 2组 C. 3组 D. 4组
-
科目: 来源: 题型:
查看答案和解析>>【题目】点(a,y1)(a+2,y2)都在反比例函数y=
 (k<0)的图象上,若y1>y2,则a的取值范围是_____.
(k<0)的图象上,若y1>y2,则a的取值范围是_____.
相关试题

