【题目】如图,点C,E,F,B在同一直线上,点A,D在BC异侧,AB∥CD,AE=DF,∠A=∠D.
(1)求证:AB=CD;
(2)若AB=CF,∠B=40°,求∠D的度数.

参考答案:
【答案】(1)AB=CD(2)70°
【解析】
(1)根据平行线的性质求出∠B=∠C,根据AAS推出△ABE≌△CDF,根据全等三角形的性质得出即可;
(2)根据全等得出AB=CD,BE=CF,∠B=∠C,求出CF=CD,推出∠D=∠CFE,即可求出答案.
(1)证明:∵AB∥CD,
∴∠B=∠C,
在△ABE和△CDF中,
∠B=∠C,AE=DF ,∠A=∠D.
∴△AEB≌△DFC.
∴AB=CD.
(2)∵AB=CD,
AB=CF,
∴CD=CF,
∵∠B=∠C=40°,
∴∠D=(180°-40°)÷2=70°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A(3,1),B(8,5),若用(3,1)→(3,3)→(5,3)→(5,4)→(8,4)→(8,5)表示由A到B的一种走法,并规定从A到B只能向上或向右走,请用上述表示法写出另两种走法,并判断这几种走法的路程是否相等。
-
科目: 来源: 题型:
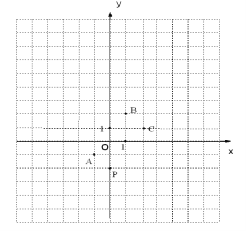
查看答案和解析>>【题目】如图,在平面直角坐标系中,一颗棋子从点P处开始依次关于点A、B、C作循环对称跳动,即第一次跳到点P关于点A的对称点M处,接着跳到点M关于点B的对称点N处,第三次再跳到点N关于点C的对称点处,….如此下去。
(1)在图中画出点M、N,并写出点M、N的坐标:
(2)求经过第2010次跳动之后,棋子落点的位置。
-
科目: 来源: 题型:
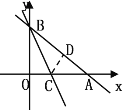
查看答案和解析>>【题目】如图,一次函数的图像与x轴、y轴分别交于A、B两点,且A、B的坐标分别为(4,0),(0,3).
(1)求一次函数的表达式.
(2)点C在线段OA上,沿BC将△OBC翻折,O点恰好落在AB上的D处,
求直线BC的表达式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各等式中成立的是( )
A.﹣ =﹣2
=﹣2
B.﹣ =﹣0.6
=﹣0.6
C.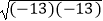 =﹣13
=﹣13
D. =±6
=±6 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在平面直角坐标系中,点A、B在x轴上,AB⊥BC,AO=OB=2,BC=3
(1)写出点A、B、C的坐标.
(2)如图②,过点B作BD∥AC交y轴于点D,求∠CAB+∠BDO的大小.
(3)如图③,在图②中,作AE、DE分别平分∠CAB、∠ODB,求∠AED的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,第一次将三角形
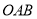 变换成三角形
变换成三角形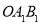 ,第二次将三角形
,第二次将三角形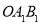 变换成三角形
变换成三角形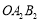 ,第三次将三角形变换成三角形
,第三次将三角形变换成三角形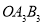 ,已知
,已知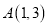 ,
,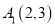 ,
, ,
, ,
,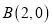 ,
,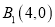 ,
,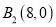 ,
, .
.(1)观察每次变换前后的三角形,找出规律,按这些变换规律将三角形
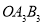 变换成三角形
变换成三角形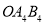 ,求
,求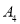 和
和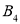 的坐标;
的坐标;(2)若按第(1)题的规律将三角形
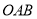 进行了
进行了 次变换,得到三角形
次变换,得到三角形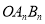 ,请推测
,请推测 和
和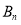 的坐标.
的坐标.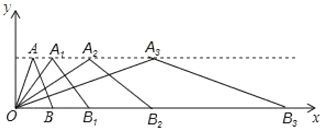
相关试题

