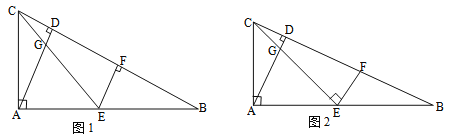
【题目】在△ABC中,∠CAB=90°,AD⊥BC于点D,点E为AB的中点,EC与AD交于点G,点F在BC上.
(1)如图1,若AC:AB=1:2,EF⊥CB,求证:EF=CD;
(2)如图2,若AC:AB=1: ![]() ,EF⊥CE,求EF: EG的值.
,EF⊥CE,求EF: EG的值.
参考答案:
【答案】(1)证明见解析;(2)![]()
【解析】(1)根据同角的余角相等得出∠CAD=∠B,根据AC:AB=1:2及点E为AB的中点,得出AC=BE,再利用AAS证明△ACD≌△BEF,即可得出EF=CD;
(2)作EH⊥AD于H,EQ⊥BC于Q,先证明四边形EQDH是矩形,得出∠QEH=90°,则∠FEQ=∠GEH,再由两角对应相等的两三角形相似证明△EFQ∽△EGH,得出EF:EG=EQ:EH,然后在△BEQ中,根据正弦函数的定义得出EQ=![]() BE,在△AEH中,根据余弦函数的定义得出EH=
BE,在△AEH中,根据余弦函数的定义得出EH=![]() AE,又BE=AE,进而求出EF:EG的值.
AE,又BE=AE,进而求出EF:EG的值.
解:(1)证明:如图所示,∵AC:AB=1:2,点E为AB的中点,∴AC=BE,
∵AD⊥BC,∠CAB=90°,
∴∠B+∠BAD=∠DAC+∠BAD=90°,∴∠B=∠DAC ,
又∵AD⊥BC,EF⊥CB,∴∠ADC=∠BFE=90°,
∴△EFB≌△CDA(AAS)
∴EF=CD.
(2)过点E作EMBD,EN⊥AD,如图2所示,

∵AD⊥BC ∴∠NEM=90° ∵CE⊥EF ∴∠NEG=∠MEF
∵∠ENG=∠EMF=90°,∴△EMF∽△ENG,∴![]() ,
,
∵AD⊥BC,AC:AB=1: ![]() ,∴∠B=30°,∴∠NAE=60°
,∴∠B=30°,∴∠NAE=60°
∴EN=![]() AE,同理可得EM=
AE,同理可得EM=![]() BE,
BE,
∵点E为AB的中点,∴AE=BE,
∴![]() =
=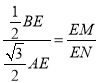 =
=![]() .
.
“点睛”本题考查了相似三角形的判定和性质、全等三角形的判定和性质、矩形的判定和性质,解直角三角形,综合性较强,有一定难度.解题的关键是作辅助线,构造相似三角形,并且证明四边形EQDH是矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】线段CD 是由线段 AB 平移得到的,点 A1, 0的对应点为C 2, 1 ,则点 B 0,3的对应点 D 的坐标是_____________
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算错误的是( )
A.0﹣(﹣5)=5
B.(﹣3)﹣(﹣5)=2??
C.
D.(﹣36)÷(﹣9)=﹣4 -
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)(﹣8)﹣1
(2)2﹣2÷(﹣ )×3
)×3
(3)12﹣(﹣18)+(﹣7)﹣15
(4)﹣32+(﹣2)2
(5)(﹣ +
+  ﹣
﹣  )×(﹣24)
)×(﹣24)
(6)(﹣6)2×| ﹣
﹣  |﹣(﹣3)
|﹣(﹣3) -
科目: 来源: 题型:
查看答案和解析>>【题目】挑战自我!
下图是由一些火柴棒搭成的图案:
(1)摆第①个图案用根火柴棒,
摆第②个图案用根火柴棒,
摆第③个图案用根火柴棒.
(2)按照这种方式摆下去,摆第n个图案用多少根火柴棒?
(3)计算一下摆121根火柴棒时,是第几个图案? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动,它从A处出发看望B、C、D处的其它甲虫.规定:向上向右走为正,向下向左走为负,如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(﹣1,﹣4).其中第一数表示左右方向,第二个数表示上下方向,那么图中
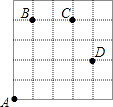
(1)A→C( , ),B→D( , );
(2)若这只甲虫的行走路线为A→B→C→D,请计算该甲虫走过的路程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知光的速度为300 000 000米/秒,太阳光到达地球的时间大约是500秒,试计算太阳与地球的距离大约是千米.(结果用科学记数法表示)
相关试题

