【题目】探究与发现:
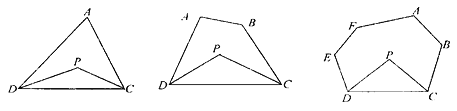
图1 图2 图3
(1)探究一:三角形的一个内角与另两个内角的平分线所夹的角之间的关系
已知:如图1,在△ADC中,DP、CP分别平分∠ADC和∠ACD,
试探究∠P与∠A的数量关系,并说明理由.
(2)探究二:四边形的两个个内角与另两个内角的平分线所夹的角之间的关系
已知:如图2,在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,
试探究∠P与∠A+∠B的数量关系,并说明理由.
(3)探究三:六边形的四个内角与另两个内角的平分线所夹的角之间的关系
已知:如图3,在六边形ABCDEF中,DP、CP分别平分∠EDC和∠BCD,
请直接写出∠P与∠A+∠B+∠E+∠F的数量关系:__ __ __.
参考答案:
【答案】(1)∠P=90°+![]() ∠A (2) ∠P=
∠A (2) ∠P=![]() (∠A+∠B)(3)∠P=
(∠A+∠B)(3)∠P=![]() (∠A+∠B+∠E+∠F)-180°
(∠A+∠B+∠E+∠F)-180°
【解析】试题分析:探究一:根据角平分线的定义可得∠PDC=![]() ∠ADC,∠PCD=
∠ADC,∠PCD=![]() ∠ACD,然后根据三角形内角和定理列式整理即可得解;
∠ACD,然后根据三角形内角和定理列式整理即可得解;
探究二:根据四边形的内角和定理表示出∠ADC+∠BCD,然后同理探究二解答即可;
探究三:根据六边形的内角和公式表示出∠ADC+∠BCD,然后同理探究二解答即可.
试题解析:探究一:∵DP、CP分别平分∠ADC和∠ACD,
∴∠PDC=![]() ∠ADC,∠PCD=
∠ADC,∠PCD=![]() ∠ACD,
∠ACD,
∴∠DPC=180°-∠PDC-∠PCD,
=180°-![]() ∠ADC-
∠ADC-![]() ∠ACD,
∠ACD,
=180°-![]() (∠ADC+∠ACD),
(∠ADC+∠ACD),
=180°-![]() (180°-∠A),
(180°-∠A),
=90°+![]() ∠A;
∠A;
探究二:∵DP、CP分别平分∠ADC和∠BCD,
∴∠PDC=![]() ∠ADC,∠PCD=
∠ADC,∠PCD=![]() ∠BCD,
∠BCD,
∴∠DPC=180°-∠PDC-∠PCD,
=180°-![]() ∠ADC-
∠ADC-![]() ∠BCD,
∠BCD,
=180°-![]() (∠ADC+∠BCD),
(∠ADC+∠BCD),
=180°-![]() (360°-∠A-∠B),
(360°-∠A-∠B),
=![]() (∠A+∠B);
(∠A+∠B);
探究三:六边形ABCDEF的内角和为:(6-2)180°=720°,
∵DP、CP分别平分∠ADC和∠ACD,
∴∠P=![]() ∠ADC,∠PCD=
∠ADC,∠PCD=![]() ∠ACD,
∠ACD,
∴∠P=180°-∠PDC-∠PCD,
=180°-![]() ∠ADC-
∠ADC-![]() ∠ACD,
∠ACD,
=180°-![]() (∠ADC+∠ACD),
(∠ADC+∠ACD),
=180°-![]() (720°-∠A-∠B-∠E-∠F),
(720°-∠A-∠B-∠E-∠F),
=![]() (∠A+∠B+∠E+∠F)-180°,
(∠A+∠B+∠E+∠F)-180°,
即∠P=![]() (∠A+∠B+∠E+∠F)-180°.
(∠A+∠B+∠E+∠F)-180°.
考点: 1.多边形内角与外角;2.三角形内角和定理.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某件商品的成本价为15元,据市场调查得知,每天的销量y(件)与价格x(元)有下列关系:
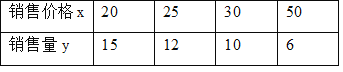
(1)根据表中数据,在直角坐标系中描出实数对(x,y)的对应点,并画出图象;
(2)猜测确定y与x间的关系式.
(3)设总利润为W元,试求出W与x之间的函数关系式,若售价不超过30元,求出当日的销售单价定为多少时,才能获得最大利润?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在下列每个图形中(每个图形都各自独立),是否存在相似的三角形,如果存在,把它们用字母表示出来,并简要说明识别的根据.

-
科目: 来源: 题型:
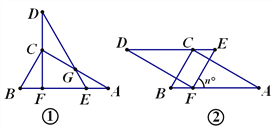
查看答案和解析>>【题目】已知△ABC、△DEF是两个完全一样的三角形,其中∠ACB=∠DFE=90°,∠A=∠D=30°.
(1)将它们摆成如图①的位置(点E、F在AB上,点C在DF上,DE与AC相交于点G).求∠AGD的度数.
(2)将图①的△ABC固定,把△DEF绕点F按逆时针方向旋转n°.
①当△DEF旋转到DE∥AB的位置时(如图2), n = ;
②若由图①旋转后的EF能与△ABC的一边垂直,则n的值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起(其中,∠A=60°,∠D=30°;∠E=∠B=45°):
(1)①若∠DCE=45°,则∠ACB的度数为 ;
②若∠ACB=140°,求∠DCE的度数;
(2)由(1)猜想∠ACB与∠DCE的数量关系,并说明理由.
(3)当∠ACE<180°且点E在直线AC的上方时,这两块三角尺是否存在一组边互相平行?若存在,请直接写出∠ACE角度所有可能的值(不必说明理由);若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为积极响应南充市创建“全国卫生城市”的号召,某校1 500名学生参加了卫生知识竞赛,成绩记为A、B、C、D四等。从中随机抽取了部分学生成绩进行统计,绘制成如下两幅不完整的统计图表,根据图表信息,以下说法不正确的是( )
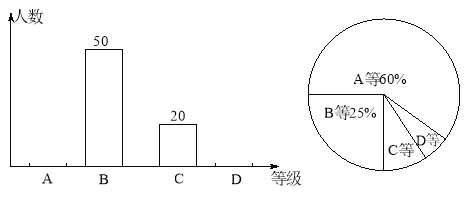
A.样本容量是200
B.D等所在扇形的圆心角为15°
C.样本中C等所占百分比是10%
D.估计全校学生成绩为A等大约有900人
-
科目: 来源: 题型:
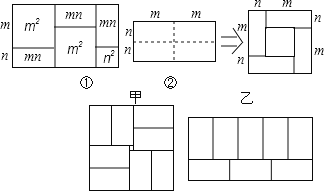
查看答案和解析>>【题目】有许多代数恒等式可以用图形的面积来表示,如图①,它表示了(2m+n)(m+n)=2m2+3mn+n2.
(1)图②是将一个长2m、宽2n的长方形,沿图中虚线平方为四块小长方形,然后再拼成一个正方形,请你观察图形,写出三个代数式(m+n)2、(m-n)2、mn关系的等式: ;
(2)若已知x+y=7、xy=10,则(x-y) 2= ;
(3)小明用8个一样大的长方形(长acm,宽bcm)拼图,拼出了如图甲、乙的两种图案,图案甲是一个正方形,图案乙是一个大的长方形,图案甲的中间留下了边长是2cm的正方形小洞,则(a+2b)2-8ab的值为 .
相关试题

