Question

【题目】如图，直线y=x+2与抛物线y=ax2+bx+6（a≠0）相交于A（，）和B（4，m），点P是线段AB上异于A、B的动点，过点P作PC⊥x轴于点D，交抛物线于点C．

（1）求抛物线的解析式；

（2）是否存在这样的P点，使线段PC的长有最大值，若存在，求出这个最大值；若不存在，请说明理由；

（3）求PAC为直角三角形时点P的坐标．

Answer 1

【答案】解：（1）∵B（4，m）在直线y=x+2上

∴m=6,即B(4，6)

∵A和B（4，6）在抛物线上

∴

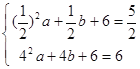
解得

∴抛物线的解析式；

（2）存在.

设动点P的坐标为（n，n+2），点C的坐标为（n，2n2-8n+6），

∴PC=（n+2）-（2n2-8n+6），

=-2n2+9n-4，

=-2（n-）+

∵-2＜0，

∴当n=时，线段PC最大且为．

【解析】试题分析：（1）已知B（4，m）在直线y=x+2上，可求得m的值，抛物线图象上的A、B两点坐标，可将其代入抛物线的解析式中，通过联立方程组即可求得待定系数的值．

（2）要弄清PC的长，实际是直线AB与抛物线函数值的差．可设出P点横坐标，根据直线AB和抛物线的解析式表示出P、C的纵坐标，进而得到关于PC与P点横坐标的函数关系式，根据函数的性质即可求出PC的最大值．

（3）当△PAC为直角三角形时，根据直角顶点的不同，有三种情形，需要分类讨论，分别求解．

试题解析：（1）∵B（4，m）在直线y=x+2上，

∴m=4+2=6，

∴B（4，6），

∵A（， ）、B（4，6）在抛物线y= +bx+6上，

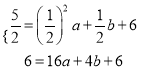∴，解得，

∴抛物线的解析式为y=﹣8x+6；

（2）设动点P的坐标为（n，n+2），则C点的坐标为（n， ﹣8n+6），

∴PC=（n+2）﹣（﹣8n+6），

=﹣+9n﹣4，

=，

∵PC＞0，

∴当n=时，线段PC最大值为；

（3）∵△PAC为直角三角形，

i）若点P为直角顶点，则∠APC=90°．

由题意易知，PC∥y轴，∠APC=45°，因此这种情形不存在；

ii）若点A为直角顶点，则∠PAC=90°．

如答图3﹣1，过点A（， ）作AN⊥x轴于点N，则ON=，AN=．

过点A作AM⊥直线AB，交x轴于点M，则由题意易知，△AMN为等腰直角三角形，

∴MN=AN=，∴OM=ON+MN=+=3，

∴M（3，0）．

设直线AM的解析式为：y=kx+b，

则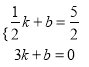： ，解得，

∴直线AM的解析式为：y=﹣x+3①，

又抛物线的解析式为：y=﹣8x+6②，

联立①②式，解得：x=3或x=（与点A重合，舍去），

∴C（3，0），即点C、M点重合．

当x=3时，y=x+2=5，

∴（3，5）；

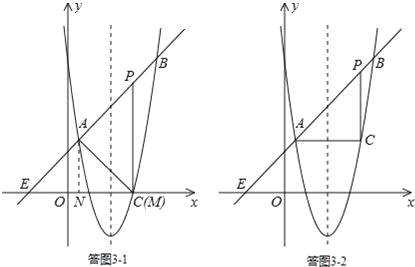
iii）若点C为直角顶点，则∠ACP=90°．

∵y=﹣8x+6=，

∴抛物线的对称轴为直线x=2．

如答图3﹣2，作点A（， ）关于对称轴x=2的对称点C，

则点C在抛物线上，且C（， ）．

当x=时，y=x+2=．

∴（， ）．

∵点（3，5）、（， ）均在线段AB上，

∴综上所述，△PAC为直角三角形时，点P的坐标为（3，5）或（， ）．