【题目】如图,△A′B′C′是由△ABC平移后得到的,已知△ABC中一点P(x0,y0)经平移后对应点P′(x0+5,y0-2).
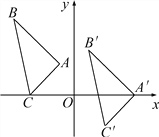
(1)已知A(-1,2),B(-4,5),C(-3,0),请写出A′、B′、C′的坐标;
(2)试说明△A′B′C′是如何由△ABC平移得到的;
(3)请直接写出△A′B′C′的面积为6.
参考答案:
【答案】(1)A′为(4,0)、B′为(1,3)、C′为(2,-2);
(2)△ABC先向右平移5个单位,再向下平移2个单位(或先向下平移2个单位,再向右平移5个单位);
(3)△A′B′C′的面积为6.
【解析】试题分析: (1)根据点P(x0,y0)经平移后对应点为P′(x0+5,y0-2)可得A,B,C三点的坐标变化规律,进而可得答案,
(2)根据点的坐标的变化规律可得△ABC先向右平移5个单位,再向下平移2个单位,(3)把△A′B′C′放在一个矩形内,利用矩形的面积减去周围多余三角形的面积即可
试题解析:(1)A′为(4,0),B′为(1,3),C′为(2,-2),
(2)△ABC先向右平移5个单位,再向下平移2个单位(或先向下平移2个单位,再向右平移5个单位),
(3)△A′B′C′的面积为6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)在东营市中小学标准化建设工程中,某学校计划购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元.
(1)求每台电脑、每台电子白板各多少万元?
(2)根据学校实际,需购进电脑和电子白板共30台,总费用不超过30万元,但不低于28万元,请你通过计算求出有几种购买方案,哪种方案费用最低.
-
科目: 来源: 题型:
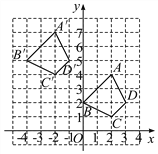
查看答案和解析>>【题目】四边形ABCD各顶点的坐标分别为A(2,4)、B(0,2)、C(2,1)、D(3,2),将四边形向左平移4个单位长度,再向上平移3个单位长度,得到四边形A′B′C′D′.
(1)四边形A′B′C′D′与四边形ABCD对应点的横坐标有什么关系?纵坐标呢?分别写出A′B′C′D′的坐标;
(2)如果将四边形A′B′C′D′看成是由四边形ABCD经过一次平移得到的,请指出这一平移的方向和距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点 A(x,y),若 xy=0,那么点 A 在___________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中正确的有( )
①如果|a|=|b|,那么a=b;
②两条直线被第三条直线所截,同位角相等;
③如果三条直线两两相交,那么可把一个平面最多分成6个部分;
④不是对顶角的角可以相等
A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种商品的进价为800元,出售是标价为1200元,后来由于该商品积压,商品准备打折销售,但是保证利润率不低于5%,则至少可打( )
A.6折B.7折C.8折D.9折
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l1在平面直角坐标系中,直线l1与y轴交于点A,点B(﹣3,3)也在直线l1上,将点B先向右平移1个单位长度,再向下平移2个单位长度得到点C,点C恰好也在直线l1上.

(1)求点C的坐标和直线l1的解析式;
(2)若将点C先向左平移3个单位长度,再向上平移6个单位长度得到点D,请你判断点D是否在直线l1上;
(3)已知直线l2:y=x+b经过点B,与y轴交于点E,求△ABE的面积.
相关试题

