【题目】为培养学生自主意识,拓宽学生视野,促进学习与生活的深度融合我市某中学决定组织部分学生去青少年综合实践基地进行综合实践活动在参加此次活动的师生中,若每位老师带17个学生,还剩12个学生没人带;若每位老师带18个学生,就有一位老师少带4个学生现有甲、乙两种大客车它们的载客量和租金如表所示
甲种客车 | 乙种客车 | |
载客量(人/辆) | 30 | 42 |
租金(元/辆) | 300 | 400 |
学校计划此实践活动的租车总费用不超过3100元,为了安全每辆客车上至少要有2名老师.
(1)参加此次综合实践活动的老师和学生各有多少人?
(2)既要保证所有师生都有车坐,又要保证每辆客车上至少要有2名老师,租用客车总数为多少辆?
(3)你能得出哪几种不同的租车方案?其中哪种租车方案最省钱?请说明理由.
参考答案:
【答案】(1)16,284;(2)8;(3)共有3种租车方案,最节省费用的租车方案是:租用甲种客车3辆,乙种客车5辆,理由见解析.
【解析】
(1)设老师有x名,学生有y名,根据等量关系:若每位老师带17个学生,还剩12个学生没人带;若每位老师带18个学生,就有一位老师少带4个学生,列出方程组,解方程组即可得答案;(2)由(1)中的老师人数可确定出最多需要的车数,再根据总人数及最多的是42座可确定出汽车总数的最小值,即可得答案;(3)设租用x辆乙种客车,则甲种客车数为(8-x)辆,由题意可得400x+300(8-x)≤3100,即可求出x的取值范围,分析即可得答案.
(1)设老师有x名,学生有y名.
依题意,列方程组为![]() ,
,
解之得:![]() ,
,
答:老师有16名,学生有284名;
(2)∵每辆客车上至少要有2名老师,
∴汽车总数不能大于8辆;
∵要保证300名师生有车坐,
∴汽车总数不能小于![]() (取整为8)辆,
(取整为8)辆,
∴汽车总数为8辆.
(3)设租用x辆乙种客车,则甲种客车数为(8-x)辆,
∵车总费用不超过3100元,
∴400x+300(8-x)≤3100,
解得:x≤7,
为使300名师生都有座,
∴42x+30(8-x)≥300,
解得:x≥5,
∴5≤x≤7(x为整数),
∴共有3种租车方案:
方案一:租用甲种客车3辆,乙种客车5辆,租车费用为2900元;
方案二:租用甲种客车2辆,乙种客车6辆,租车费用为3000元;
方案三:租用甲种客车1辆,乙种客车7辆,租车费用为3100元;
故最节省费用的租车方案是:租用甲种客车3辆,乙种客车5辆.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
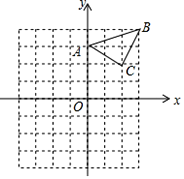
(1)△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是 ;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是 ;(画出图形)
(3)△A2B2C2的面积是 平方单位.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司投资新建了一商场,共有商铺30间,据推测,当每间的年租金定为10万元时,可全部租出,若每间的年租金每增加5000元,少租出商铺1间,该公司要为租出的商铺每间每年交各种费用1万元,未租出的商铺每间每年交各种费用5000元.
(1)当每间商铺的年租金定为12万元时,能租出多少间?
(2)当每间商铺的年租金定为多少万元时,该公司的年收益为285万元?(收益=租金﹣各种费用)
-
科目: 来源: 题型:
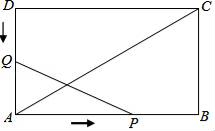
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从点A开始向点B以2cm/s的速度移动,点Q沿DA边从点D开始向点A以1cm/s的速度移动,如果P、Q同时出发,用t(s)表示移动的时间(0≤t≤6),那么:
(1)当t为何值时,△QAP是等腰直角三角形?
(2)当t为何值时,以点Q、A、P为顶点的三角形与△ABC相似?
-
科目: 来源: 题型:
查看答案和解析>>【题目】本学期实验中学组织开展课外兴趣活动,各活动小班根据实际情况确定了计划组班人数,并发动学生自愿报名,报名人数与计划人数的前5位情况如下:
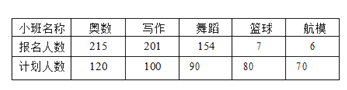
若用同一小班的计划人数与报名人数的比值大小来衡量进入该班的难易程度,学生中对于进入各活动小班的难易有以下预测:①篮球和航模都能进;②舞蹈比写作容易;③写作比奥数容易;④舞蹈比奥数容易.则预测正确的有___________(填序号即可).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某风景点的团体购买门票票价如下:

今有甲、乙两个旅行团,已知甲团人数少于 50 人,乙团人数不超过 100 人.若分别购票,两团共计应付门票费 1950 元,若合在一起作为一个团体购票,总计应付门票 费 1545 元.
(1)请你判断乙团的人数是否也少于 50 人;
(2)求甲、乙两旅行团各有多少人?
(3)甲旅行团单独购票,有无更省钱的方案?说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】请你认真阅读下面的小探究系列,完成所提出的问题.
(1)如图1,将角尺放在正方形ABCD上,使角尺的直角顶点E与正方形ABCD的顶点D重合,角尺的一边交CB于点F,将另一边交BA的延长线于点G.求证:EF=EG.
(2)如图2,移动角尺,使角尺的顶点E始终在正方形ABCD的对角线BD上,其余条件不变,请你思考后直接回答EF和EG的数量关系:EF EG(用“=”或“≠”填空)
(3)运用(1)(2)解答中所积累的活动经验和数学知识,完成下题:如图3,将(2)中的“正方形ABCD”改成“矩形ABCD”,使角尺的一边经过点A(即点G、A重合),其余条件不变,若AB=4,BC=3,求
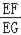 的值.
的值.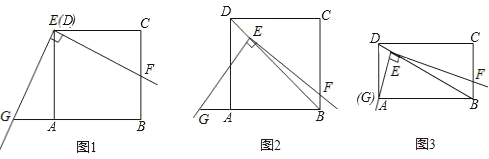
相关试题

