【题目】如图①是一种包装盒的表面展开图,将它围起来可得到一个几何体的模型.
(1)请说出这个几何体模型的最确切的名称是__ __;
(2)如图②是根据 a,h的取值画出的几何体的主视图和俯视图(图中的粗实线表示的正方形(中间一条虚线)和三角形),请在网格中画出该几何体的左视图;
(3)在(2)的条件下,已知h=20 cm,求该几何体的表面积.

参考答案:
【答案】(1)直三棱柱;(2)图见解析;(3)S表面积=600+400![]() (cm2)
(cm2)
【解析】(8分)如图①是一种包装盒的表面展开图,将它围起来可得到一个几何体的模型.
(1)请说出这个几何体模型的最确切的名称是__直三棱柱 __;
(2)图略 (3)由题意可得:a=![]() =
=![]() =10
=10![]() ,S表面积=
,S表面积=![]() ×(10
×(10![]() )2×2+2×10
)2×2+2×10![]() ×20+202=600+400
×20+202=600+400![]() (cm2)
(cm2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知线段AB的长为a,延长线段AB至点C,使BC=
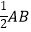 .
. 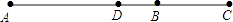
(1)求线段AC的长(用含a的代数式表示);
(2)取线段AC的中点D,若DB=3,求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.a2a3=a6
B.(﹣a3)2=﹣a6
C.(﹣3a2)2=6a4
D.(﹣a+b)(a+b)=b2﹣a2 -
科目: 来源: 题型:
查看答案和解析>>【题目】(12分)如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D.点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到C时,两点都停止.设运动时间为t秒.
(1)求线段CD的长;
(2)设△CPQ的面积为S,求S与t之间的函数关系式,并确定在运动过程中是否存在某一时刻t,使得S△CPQ∶S△ABC=9∶100?若存在,求出t的值;若不存在,说明理由;
(3)当t为何值时,△CPQ为等腰三角形?

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法错误的是( )
A. 对角线互相平分的四边形是平行四边形
B. 两组对边分别相等的四边形是平行四边形
C. 一组对边平行且相等的四边形是平行四边形
D. 一组对边相等,另一组对边平行的四边形是平行四边形
-
科目: 来源: 题型:
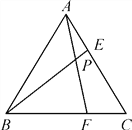
查看答案和解析>>【题目】如图,等边三角形ABC的边长为6,在AC,BC边上各取一点E,F,连接AF,BE相交于点P,且AE=CF.
(1)求证:AF=BE,并求∠FPB的度数;
(2)若AE=2,试求AP·AF的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式﹣2x<4的解集是( )
A. x>2 B. x<2 C. x<﹣2 D. x>﹣2
相关试题

