【题目】已知关于x的一元二次方程x2﹣(m+3)x+m=0.
(1)求证:无论实数m取何值,方程总有两个不相等的实数根;
(2)若方程一个根是2,求m的值.
参考答案:
【答案】(1)证明见解析;(2)-2.
【解析】(1)根据方程的系数结合根的判别式,可得出△=(m+1)2+8>0,由此即可证出:无论实数m取何值,方程总有两个不相等的实数根;
(2)将x=2代入原方程,即可求出m的值.
(1)△=[﹣(m+3)]2﹣4×1×m=(m+1)2+8.
∵(m+1)2≥0,∴(m+1)2+8>0,即△>0,∴无论实数m取何值,方程总有两个不相等的实数根;
(2)当x=2时,原方程为4﹣2(m+3)+m=0,解得:m=﹣2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠1与∠2互余,∠2与∠3互补,∠1=58°,则∠3=( )
A.58°
B.148°
C.158°
D.32° -
科目: 来源: 题型:
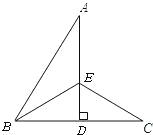
查看答案和解析>>【题目】如图,∠ABC=50°,AD垂直且平分BC于点D,∠ABC的平分线BE交AD于点E,连接EC,则∠AEC的度数是( )
A.50°
B.25°
C.80°
D.115° -
科目: 来源: 题型:
查看答案和解析>>【题目】共享单车为市民出行带来了方便,某单车公司第一个月投放1000辆单车,计划第三个月投放单车数量比第一个月多440辆.设该公司第二、三连个月投放单车数量的月平均增长率为x,则所列方程正确的是( )
A.1000(1+x)2=440B.1000(1+x)2=1000
C.1000(1+2x)=1000+440D.1000(1+x)2=1000+440
-
科目: 来源: 题型:
查看答案和解析>>【题目】线段EF是由线段PQ平移得到的,点P(-1,4)的对应点为E(4,7),则点Q(-3,1)的对应点F的坐标为( )
A. (-8,-2) B. (-2,2) C. (2,4) D. (-6,-1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.
(1)求出每天的销售利润y(元)与销售单价x(元)之间的函数关系式;
(2)如果该企业要使每天的销售利润不低于4000元,且每天的总成本不超过7000元,那么销售单价应控制在什么范围内?(每天的总成本=每件的成本×每天的销售量)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A的坐标为(﹣1,﹣2),将OA绕原点O逆时针旋转180°得到OA′,点A′的坐标为(a,b),则a﹣b等于( )
A.1
B.﹣1
C.3
D.﹣3
相关试题

