【题目】如图,在Rt△ABC中,∠ACB=90°,D为AB的中点,AE∥CD,CE∥AB,连接DE交AC于点O. 
(1)证明:四边形ADCE为菱形;
(2)证明:DE=BC.
参考答案:
【答案】
(1)证明:∵AE∥CD,CE∥AB,
∴四边形ADCE是平行四边形,
∵∠ACB=90°,D为AB的中点,
∴CD= ![]() AB=AD,
AB=AD,
∴四边形ADCE为菱形
(2)证明:∵四边形ADCE为菱形,
∴AC⊥DE,
∵∠ACB=90°,
∴AC⊥BC,
∴DE∥BC,
又∵CE∥AB,
∴四边形BCED是平行四边形,
∴DE=BC
【解析】(1)先证明四边形ADCE是平行四边形,再由直角三角形斜边上的中线性质得出CD= ![]() AB=AD,即可得出四边形ADCE为菱形;(2)由菱形的性质得出AC⊥DE,证出DE∥BC,再由CE∥AB,证出四边形BCED是平行四边形,即可得出结论.
AB=AD,即可得出四边形ADCE为菱形;(2)由菱形的性质得出AC⊥DE,证出DE∥BC,再由CE∥AB,证出四边形BCED是平行四边形,即可得出结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知矩形ABCD的长和宽分别为16cm和12cm,连接其对边中点,得到四个矩形,顺次连接矩形AEFG各边中点,得到菱形l1;连接矩形FMCH对边中点,又得到四个矩形,顺次连接矩形FNPQ各边中点,得到菱形l2;…如此操作下去,则l4的面积是cm2 .
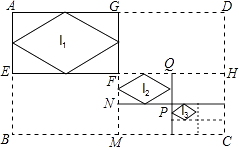
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB表示路灯,当身高为1.6米的小名站在离路灯1.6的D处时,他测得自己在路灯下的影长DE与身高CD相等,当小明继续沿直线BD往前走到E点时,画出此时小明的影子,并计算此时小明的影长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】两枚正四面体骰子的各面上分别标有数字1,2,3,4,现在同时投掷这两枚骰子,并分别记录着地的面所得的点数为a、b.
(1)假设两枚正四面体都是质地均匀,各面着地的可能性相同,请你在下面表格内列举出所有情形(例如(1,2),表示a=1,b=2),并求出两次着地的面点数相同的概率.b
a1
2
3
4
1
(1,2)
2
3
4
(2)为了验证试验用的正四面体质地是否均匀,小明和他的同学取一枚正四面体进行投掷试验.试验中标号为1的面着地的数据如下:试验总次数
50
100
150
200
250
500
“标号1”的面着地的次数
15
26
34
48
63
125
“标号1”的面着地的频率
0.3
0.26
0.23
0.24
请完成表格(数字精确到0.01),并根据表格中的数据估计“标号1的面着地”的概率是

-
科目: 来源: 题型:
查看答案和解析>>【题目】将一副三角板按如图放置,则下列结论:
①如果∠2=30°,则有AC∥DE;
②∠BAE+∠CAD =180°;
③如果BC∥AD,则有∠2=45°;
④如果∠CAD=150°,必有∠4=∠C;
正确的有( )
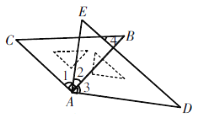
A. ①②③ B. ①②④ C. ①③④ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,下列能判定AB∥CD的条件有( )个.
(1)∠B+∠BCD=180°;(2)∠1=∠2;(3)∠3=∠4;(4)∠B=∠5.

A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正比例函数y=k1x的图象与反比例函数y=
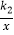 的图象的一个交点是(2,3).
的图象的一个交点是(2,3).
(1)求出这两个函数的表达式;
(2)作出两个函数的草图,利用你所作的图形,猜想并验证这两个函数图象的另一个交点的坐标;
(3)直接写出使反比例函数值大于正比例函数值的x的取值范围.
相关试题

