【题目】一农民带上若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,他手中持有的钱数(含备用零钱)y与售出的土豆千克数x的关系如图所示,结合图象回答下列问题:
(1)农民自带的零钱是______元,降价前他每千克土豆出售的价格是______元;
(2)降价后他按每千克0.8元将剩余土豆售完,这时他手中的钱(含备用零钱)是62元,求降价后的线段所表示的函数表达式并写出它的取值范围.
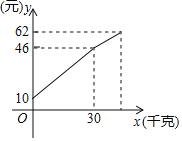
参考答案:
【答案】(1)10;1.2;(2)y=0.8x+22(30≤x≤50).
【解析】
(1)由图象可知,当x=0时,y=10,所以农民自带的零钱是10元;可设降价前每千克土豆价格为k元,则可列出农民手中钱y与所售土豆千克数x之间的函数关系式,由图象知,当x=30时,y的值,从而求出这个函数式,即可求得k值;(2)设他一共带了x千克土豆,根据题意即可得方程:0.8(x-30)+46=62,解此方程即可求得他一共带了50千克土豆,再用待定系数法求得解析式即可.
(1)由图象可知,当x=0时,y=10.
答:农民自带的零钱是10元;
设降价前每千克土豆价格为k元,
则农民手中钱y与所售土豆千克数x之间的函数关系式为:y=kx+10,
∵当x=30时,y=46,
∴46=30k+10,
解得k=1.2.
答:降价前每千克土豆价格为1.2元.
故答案为:10;1.2;
(2)设他一共带了x千克土豆,
根据题意得:0.8(x-30)+46=62,
解得:x=50.
即农民一共带了50千克土豆.
设降价后的线段所表示的函数表达式为y=k1x+b,
根据题意得![]() ,解得
,解得![]() ,
,
∴y=0.8x+22(30≤x≤50).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在利用正六面体骰子进行频率估计概率的实验中,小闽同学统计了某一结果朝上的频率,绘出的统计图如图所示,则符合图中情况的可能是( )
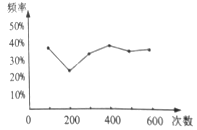
A. 朝上的点数是6的概率B. 朝上的点数是偶数的概率
C. 朝上的点数是小于4的概率D. 朝上的点数是3的倍数的概率
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点.将一块锐角为45°的直角三角板如图放置,使三角板斜边的两个端点分别与A、D重合,连接BE、EC.
 试猜想线段BE和EC的数量及位置关系,并证明你的猜想.
试猜想线段BE和EC的数量及位置关系,并证明你的猜想. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AE是ΔABC的角平分线,AD是BC边上的高。若∠ABC=34°,∠ACB=64°,则∠DAE的大小是( )
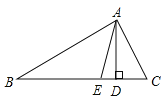
A. 5°B. 13°C. 15°D. 20°
-
科目: 来源: 题型:
查看答案和解析>>【题目】将大小不同的两个正方形按图1,图2的方式摆放.若图1中阴影部分的面积是6,图2中阴影部分的面积是5,则大正方形的面积是________.

-
科目: 来源: 题型:
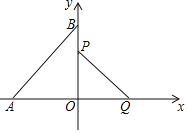
查看答案和解析>>【题目】如图,在直角坐标系中,点A、B分别在x轴和y轴上,△OBA是等腰直角三角形且AB=
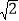 ,线段PQ=1,线段PQ的端点P从点O出发,沿△OBA的边按O→B→A→O运动一周,同时另一端点Q随之在x轴的非负半轴上运动.
,线段PQ=1,线段PQ的端点P从点O出发,沿△OBA的边按O→B→A→O运动一周,同时另一端点Q随之在x轴的非负半轴上运动.(1)求A、B两点的坐标;
(2)若P运动的路程为m,△OPA的面积为S,求S与m之间的函数关系式;
(3)当点P运动一周时,点Q运动的总路程为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】请将下面的说理过程和理由补充完整.
已知:如图,AB∥CD,∠B=∠D,说明:BF∥DE.

解:AB∥CD.(已知)
∴∠A=∠C.( ____①___)
在△ABF和△CDE中
∵∠B=∠D=90°,(已知)
∴∠A+∠AFB=90°
∠C+___②___=90°.(直角三角形的两个锐角互余)
又∵∠A=∠C,(已证).
∴∠AFB=____③_____.(_____④_____)
∴BF∥DE.( ___⑤_____)
相关试题

